前回は、アニメーションの処理を追加し、惑星の軌道計算プログラムを完成させました。
今回はこのシリーズ最終回です。プログラムを実行して、地球の軌道計算の結果を見てみたいと思います。
計算結果
前回作った惑星の軌道計算プログラムをPythonで実行してみてください。
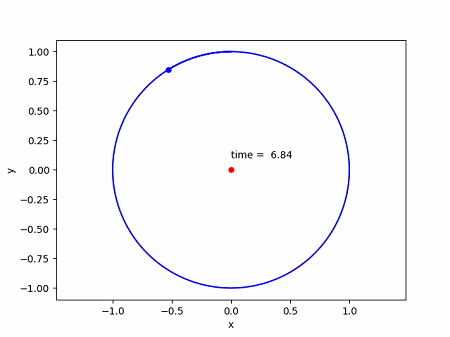
アニメーションを作成するので少し時間がかかりますが、GIFファイルが出力されて画面にも次のようなアニメーションが出力されたでしょうか。
無次元化した距離 $r_*$ = 1、速度 $v_*$ = 1 を初期値とすると、きれいな円軌道を描いていく様子が、動画でわかると思います。そして時間 $t_*$ は、6.28(= 2 $\pi$)で一周していますね。
実際の地球は完全な円軌道ではなく、少しだけ楕円形をした軌道を描いています。遠日点(太陽から一番遠い)距離が $r_*$ =1.017 で、遠日点での速度は $v_*$ = 0.9831 くらいです。プログラムの初期値を
r = np.array([0.0, 1.017])
v = np.array([-0.9831, 0.0])として計算してみてください。これがだいたいの地球の軌道ですが、見た目にはさきほどの円軌道と見分けがつきません。
では、極端に変えて、初速を半分にした場合はどうでしょうか。
r = np.array([0.0, 1.0])
v = np.array([-0.5, 0.0])として計算してみましょう。結果は次のようになります。
今度は細長い楕円軌道となりました。太陽との距離が遠いと速度は遅くなり、太陽に近づくと速く移動していく様子がわかります。ハレー彗星のような彗星が描く軌道です。
他にも惑星の軌道の形にはいくつか種類があります。太陽からの距離 $r$ での速度が $v = \sqrt{2GM/r}$ (無次元速度で $v_*=\sqrt{2/r_*}$)となるような場合、放物線軌道を描きます。
この場合は、放物線の形なので2度と太陽には戻ってきません。
また、この速度より大きいと双曲線軌道を描きます。
双曲線軌道は太陽から離れると、直線に漸近するような軌道です。「はやぶさ」などの探査機がスイングバイという方法を使って飛んでいく方向を変えたりしますが、そのときの軌道が双曲線になります。(実際には、運動している惑星を使うので、加速や減速も合わせて行われます。)
このように、初期値を変えて計算してみると、どのような条件のときに、どのような軌道を描くのか調べることができて面白いです。いろいろ条件を変えて試してみてください。
まとめ
このシリーズでは、ルンゲ=クッタ法という数値計算法を使って、プログラムを作ってきました。ルンゲ=クッタ法は簡単ですが精度が高いのでよく使われる方法です。
ある変数が時間的に変化するような微分方程式であれば、これまでの講義で作ったプログラムを変更していけば、たいがいのものは計算できると思います。身の回りの自然現象や工学的な問題をいろいろシミュレーションしてみてください。
