【科学技術計算講座2-2】ルンゲ=クッタ法の計算精度

前回はルンゲ=クッタ法という数値計算法をご紹介しました。

今回はルンゲ=クッタ法をプログラミングしてみます。そして、第１回シリーズの最後に計算した減衰振動でオイラー法と比べて計算精度がどうなっているかを比較してみたいと思います。

ルンゲ=クッタ法をプログラミング

ルンゲ=クッタ法の式

早速、Pythonでルンゲ=クッタ法をプログラミングしてみましょう。前回説明したとおり、ルンゲ=クッタ法の式は次のとおりです。

$$\frac{dy}{dt} = f(t, y) \tag{1}$$ $$k_{1} = f(t_{n},y_{n}) \tag{2}$$ $$k_{2} = f(t_{n}+\frac{\Delta t}{2},y_{n}+\frac{\Delta t}{2} k_{1})\tag{3}$$ $$k_{3} = f(t_{n}+\frac{\Delta t}{2},y_{n}+\frac{\Delta t}{2} k_{2})\tag{4}$$ $$k_{4} = f(t_{n}+\Delta t,y_{n}+\Delta t k_{3})\tag{5}$$ $$y_{n+1} = y_{n} + \frac{\Delta t}{6}(k_{1}+2 k_{2} + 2 k_{3} + k_{4})\tag{6}$$ $$t_{n+1} = t_{n} + \Delta t\tag{7}$$

減衰振動のプログラム

ここでは、以前オイラー法で作った減衰振動のプログラムをベースとしましょう。

→オイラー法の減衰振動プログラムはこちら（GitHub）

基本的なところは、このプログラムと変わりません。(2)～(7)式をforループの中に追加変更していくだけです。

    xp = x
    vp = v
    kx1 = fx(vp)
    kv1 = fv(xp, vp, k, c, m)

    xp = x + 0.5 * dt * kx1
    vp = v + 0.5 * dt * kv1
    kx2 = fx(vp)
    kv2 = fv(xp, vp, k, c, m)

    xp = x + 0.5 * dt * kx2
    vp = v + 0.5 * dt * kv2
    kx3 = fx(vp)
    kv3 = fv(xp, vp, k, c, m)

    xp = x + dt * kx3
    vp = v + dt * kv3
    kx4 = fx(vp)
    kv4 = fv(xp, vp, k, c, m)

    x = x + dt * (kx1 + 2.0 * kx2 + 2.0 * kx3 + kx4) / 6.0
    v = v + dt * (kv1 + 2.0 * kv2 + 2.0 * kv3 + kv4) / 6.0
    t = t + dt

減衰振動の運動方程式は、変位 x と速度 v の２つの変数の連立方程式になっていたので、それぞれに対して計算していきます。

まず(2)式に相当する部分。これはルンゲ=クッタ法の第１ステップで、$k_1$ を計算します。プログラムでは、

    xp = x
    vp = v
    kx1 = fx(vp)
    kv1 = fv(xp, vp, k, c, m)

の部分です。xp、vp というのは(2)式の関数 $f$ を計算するときに使う変位と速度の値です。kx1 は変位の $k_1$ を、kv1 は速度の $k_1$ を計算しています。ここで、関数 $f$ を fx、fv としています。この書き方は、これまでに出てこなかったのですが、重要な部分なので後ほど詳しく説明します。

次に、(3)式の $k_2$ を計算する部分です。

    xp = x + 0.5 * dt * kx1
    vp = v + 0.5 * dt * kv1
    kx2 = fx(vp)
    kv2 = fv(xp, vp, k, c, m)

ここでは、xp、vp は $\Delta t/ 2$ のときの値を使います。これで、$k_2$ を計算します。

その後、同じように $k_3$、$k_4$ を計算しています。

最後に、(6)、(7)式を

    x = x + dt * (kx1 + 2.0 * kx2 + 2.0 * kx3 + kx4) / 6.0
    v = v + dt * (kv1 + 2.0 * kv2 + 2.0 * kv3 + kv4) / 6.0
    t = t + dt

で計算しています。

関数の定義

さて、fx、fv というのが関数 $f$ を表しているのですが、これはどうすればよいでしょう。今回の場合、速度に対する関数は運動方程式から

$$f_v(x,v)=\frac{-kx-cv}{m} \tag{8}$$

と表されます。Pythonにも関数という概念があります。Pythonで関数を定義するには、次のように書きます。

def  関数名(引数１, 引数２, ...) :
        何かの処理
        return  返す値

引数というのは、関数に入力する値のことで、$f_v(x,v)$ の $x$、$v$ に相当します。関数の中では何かの計算処理が行われ、return文で計算結果を返します。forループと同じように関数内の処理は字下げしておいてください。

この形式で、(8)式をPythonで書くと、次のようになります。

def fv(x, v, k, c, m):
    return (-k * x - c * v) / m

関数名は fv、引数は変位 x、速度 v、ばね定数 k、減衰係数 c、質量 m です。この引数から、$(-kx-cv)/m$ を計算して返しています。これで、プログラム中の fv には引数で渡された値から計算された $(-kx-cv)/m$ の値が入ることになります。

また、変位の関数は $f_x(v) = v$ なので、

def fx(v):
    return v

と定義します。関数を定義する位置ですが、その関数を使う箇所よりも前に定義しておく必要があります。forループの中で関数を使うので、forループの前にこれらの関数定義を書いておきましょう。今回のように、同じ処理を複数の場所で何度も行うような場合には、関数を使った方が便利です。

計算実行

ルンゲ=クッタ法への変更箇所は以上です。ではこれをPythonで実行してみてください。

→ルンゲ=クッタ法の減衰振動プログラムはこちら（GitHub）

オイラー法のときと同じように、変位と速度が計算できました。

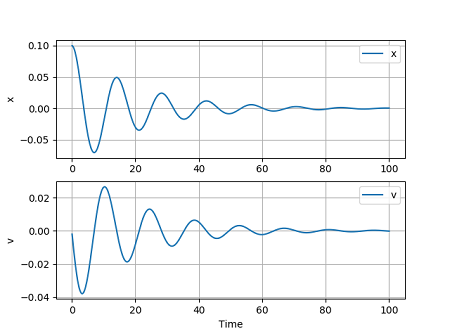
ルンゲ=クッタ法の計算精度

減衰振動の場合

結果をオイラー法と比べてみましょう。オイラー法の結果は厳密解に比べ振幅が大きかったですね。

ルンゲ=クッタ法でどうでしょうか。厳密解と比べてみます。

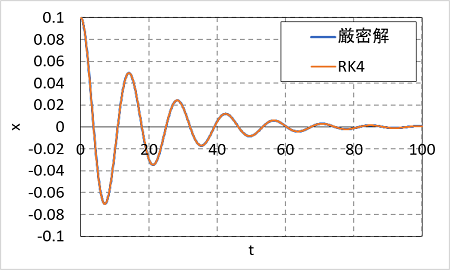
ルンゲ=クッタ法の結果は、厳密解とほぼピッタリ一致しています。

減衰がない場合

ここで、減衰がない場合を計算してみましょう。減衰係数 c = 0.0 としてオイラー法とルンゲ=クッタ法で計算してみてください。オイラー法の結果は次のようになりました。

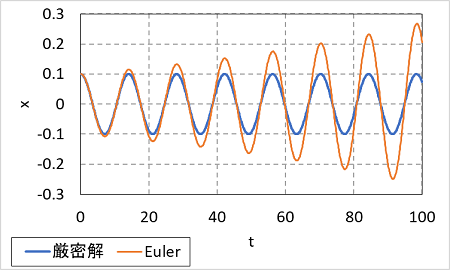
減衰がないと一定の振動がずっと続きます。ところが、オイラー法では徐々に振幅が大きくなっています。これでは、まともな結果と言えません。一方、ルンゲ=クッタ法の計算結果は次のとおりです。

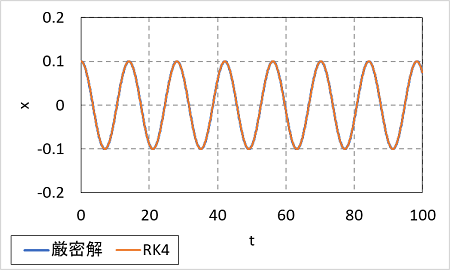
こちらはきれいな振動が続いており、厳密解とも一致しています。この比較から明らかなように、オイラー法と比べてルンゲ=クッタ法は高い精度を持っており、誤差の小さな数値計算法であることがわかります。

ただし、ルンゲ=クッタ法も時々刻々繰り返し計算していくので、誤差が蓄積しないわけではありません。また、時間刻みを大きくとりすぎると誤差が大きくなるのはオイラー法と同じです。

まとめ

減衰振動のプログラムをルンゲ=クッタ法に書き換えました。また、オイラー法の結果と比較し、高い計算精度を持っていることがわかりました。

さて、次回から地球の軌道計算に入っていきましょう。まずは、地球がどのような運動方程式にしたがって太陽の周りを運動しているのか見ていきたいと思います。

←前回　ルンゲ=クッタ法とは

→次回　惑星の運動方程式

全体の目次