目次
運動方程式シミュレーションツール
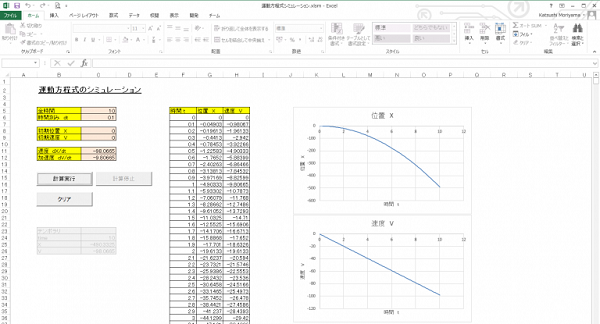
運動方程式を解くエクセルツールです。
・１次元で１物体の運動をシミュレーションできます。
・任意の運動方程式を入力することができます。
・運動方程式は4次のルンゲクッタ法で計算されます。
・計算結果として位置、速度がグラフ表示されます。
以下からダウンロードしてください。
ファイルをダウンロードする※エクセルのマクロを有効にして使用してください。
２次元で３物体までの運動をシミュレーションできるオンラインツールはこちらです。
↓
運動方程式を解くためのオンラインツールです。２次元で３物体までの運動をシミュレーションできます。入力した任意の運動方程式を解くことができます。方程式はRunge-Kutta-Fehlberg法によって解かれます。登録不要で無料でお使いいただけます。
スポンサーリンク
運動方程式
解く運動方程式は以下の形式のものです。
$$ \frac{dX}{dt} = V $$
$$ \frac{dV}{dt} = \frac{F(X,V,t)}{m}$$
$t$：時間、$X$：位置、$V$：速度、$F$：力、$m$：質量
微分方程式の解法
運動方程式は4次のルンゲクッタ法で解いています。
$$ \frac{dY}{dt} = f(t,Y)$$
$$Y_{n+1} = Y_{n} + \frac{\Delta t}{6}(k_{1}+2 k_{2} + 2 k_{3} + k_{4})$$
$$t_{n+1} = t_{n} + \Delta t$$
$$k_{1} = f(t_{n},Y_{n})$$
$$k_{2} = f(t_{n}+\frac{\Delta t}{2},Y_{n}+\frac{\Delta t}{2} k_{1})$$
$$k_{3} = f(t_{n}+\frac{\Delta t}{2},Y_{n}+\frac{\Delta t}{2} k_{2})$$
$$k_{4} = f(t_{n}+\Delta t,Y_{n}+\Delta t k_{3})$$