オンライン流体解析CATCFDzeroのチュートリアルです。ファイルから曲線データを読んで形状を定義する例題です。
目次
解析概要
図のようなボール式の逆止弁（チェックバルブ）の流れを解析します。
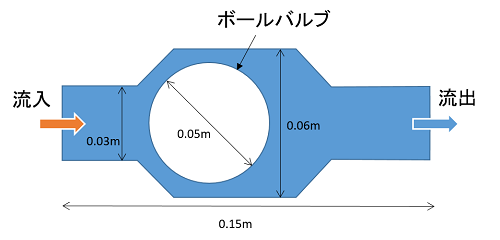
左端から水が流入し、右端から流出します。流路内には球形のボールがあります。
解析条件
- 流入：速度 1 m/s
- 流出：圧力 0 Pa
- 乱流
解析モデル
対称形状なのでハーフモデル（1/2対称モデル）として作成します。対称面には対称境界条件を与えます。
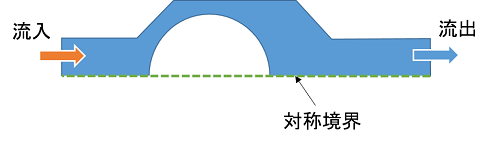
流路やボールは矩形ではないため、ブロックでは作成できません。したがって、ソリッドとして外部ファイルから形状データを読み込んで定義します。形状データファイルは、ハウジングとボールの２つ用意します。ファイルはそれぞれ下図のような点列データになっています。
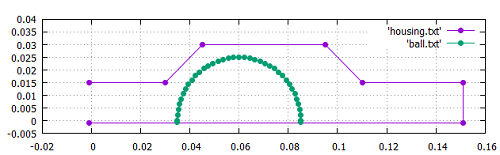
各ファイルは以下からダウンロードできます。
ハウジングの形状ファイル（housing.txt）
ボールの形状ファイル（ball.txt）
解析設定
物性の設定
[物性]メニューを開き、物性は水を選択します。
乱流のスイッチをONにします。
領域の設定
[領域]メニューで、領域のサイズ[m]を入力します。横方向Lxに 0.15 、縦方向Lyに 0.04 を入力します。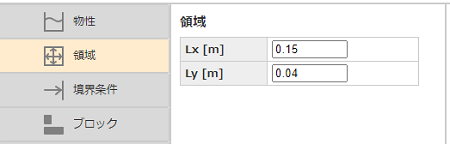
境界条件の設定
[境界条件]メニューを開き、境界条件を設定していきます。流入条件
No.１に流入条件を設定します。条件は「流入」、面は「左端」、Lmin 「0.0」、Lmax 「0.015」、値（流入速度）は「 1.0」m/sを入力します。入力したら[適用]ボタンを押してください。
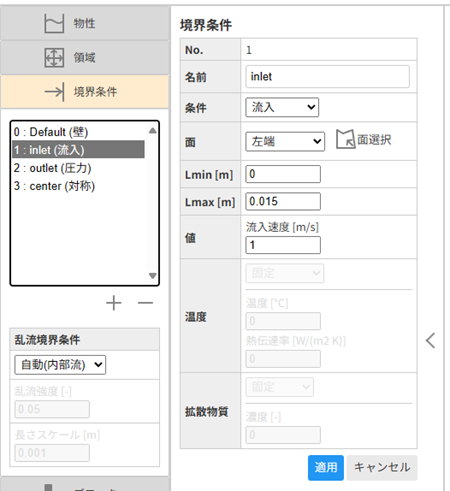
流出条件
No.２に流出のための圧力条件を設定します。条件「圧力」、面「右端」、Lmin 「0.0」、Lmax「0.015」、値（圧力）「0.0」Paを入力し、[適用]ボタンを押します。
対称条件
[+]ボタンを押し、No.3の境界条件を追加します。No.3には対称境界を設定します。条件「対称」、面「下端」、Lmin 「0.0」、Lmax「0.15」を入力します。
※[適用]ボタンを押すと、表示エリアの[結果表示]タブに境界の位置が出力されます。
今回は内部流れのため、乱流境界条件は「自動(内部流)」を選択します。
ソリッドの設定
次に[ソリッド]メニューを開き、ソリッドを２個設定します。
ハウジング
まず、[＋]ボタンを押し、１番目のソリッドを定義します。
No.1の要素の[ファイル]ボタンを押し、準備しておいたハウジングの形状ファイル（housing.txt）を読み込みます。ハウジング形状の外側が固体領域（流体が流れない領域）となるため、固体領域は「外側」を選択します。入力したら[適用]ボタンを押して、設定を確定します。
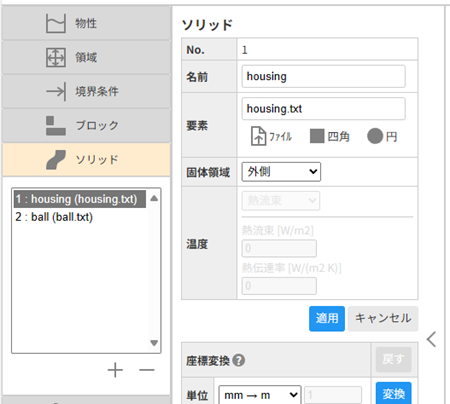
※[適用]ボタンを押すと、表示エリアの[結果表示]タブにソリッドが出力されます。
※ソリッドの形状ファイルは、設定エリアにドラッグアンドドロップしても読み込めます。
ボール
続いて、リストの[＋]ボタンを押し、No.2のソリッドを追加します。No.2では同様にボールの形状ファイル（ball.txt）を読み込みます。ボールは曲線の内側が固体領域なので、固体領域は「内側」を選択します。
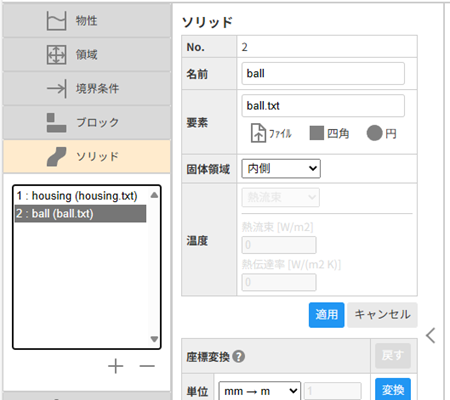
入力したら、[適用]ボタンを押して確定し、設定した位置が正しいか確認します。
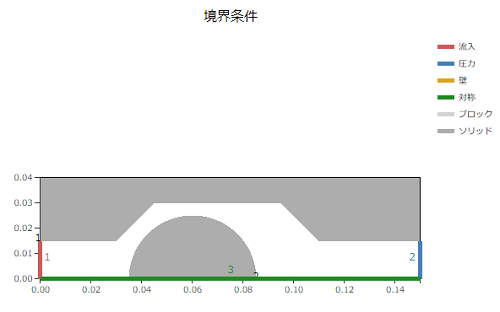
※ソリッドは要素を定義しないと、追加できないようになっています。
詳細設定
[詳細設定] メニューを開きます。メッシュ
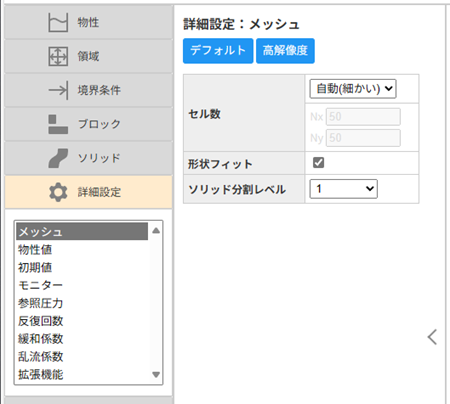
今回は、セルサイズを細かくして解像度を上げることにします。リストからメッシュを選択し、セル数の「自動（細かい）」を選択します。これで領域の長手方向が100分割になるように自動で分割されます。
緩和係数
次に、計算を安定に進めるため緩和係数を下げておきます。リストの緩和係数で、[安定化]ボタンを押します。速度Uと乱流k,εの緩和係数が「0.5」に、圧力Pの緩和係数が「0.1」に設定されます。
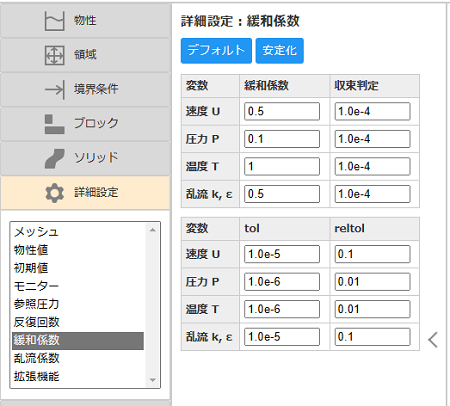
以上で解析設定は終了です。
計算実行
設定が終了したら、[計算実行]ボタンを押します。
計算が開始され、計算中は「CALCULATING...」と表示されます。
また、ボタン横のボックスに「計算中：**イタレーション **%」と現在の反復回数が表示されます。
計算が収束し終了すると、「計算終了：収束しました。」と表示されます。
結果の確認
計算が終了すると、表示エリアの[結果表示]タブに計算結果が表示されます。最初は「速度ベクトル」が表示されます。
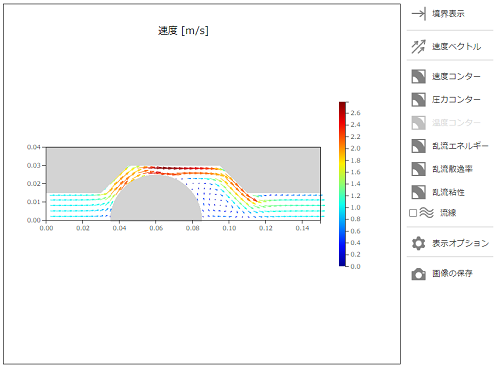
右サイドの各ボタンで見たい表示に変更します。
[流線]にチェックを入れ、[速度コンター]ボタンを押します。速度コンターと流線が同時に表示されます。ボールの後方に渦ができていることが確認できます。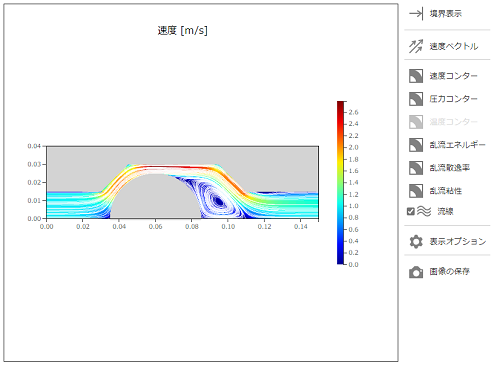
再度、見たいコンターのボタンを押します。
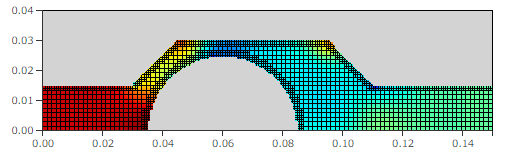
実際に計算に使われるメッシュが表示されます。ソリッドはボクセル（格子状）で表現して計算しているため、曲面は階段状になっていることがわかります。また、ソリッド表面は形状の再現性を上げるため、局所的に細分割されています。