前回は木構造と二分探索木についてお話しました。
今回は二分探索木の特徴について解説します。
目次
二分探索木の計算量
二分探索木はその形がきれいな三角形になっていれば、探索にかかる平均的な計算量は$O(\log n)$になります。ところが、木の形は挿入するデータの順番によって変わってきます。前回のデータの場合は、25→13→20→42→67→4→51→38→1→9の順にデータを挿入すると、下図のような木になりました。
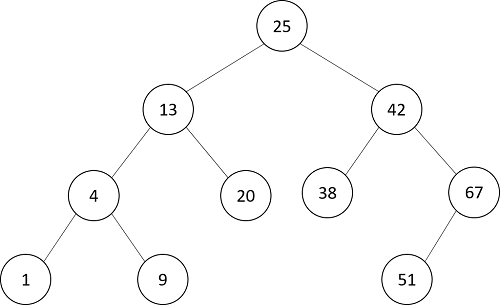
ところが、1→4→9→13→20→25→38→42→51→67 のように整列した順にデータを挿入すると、1をルートとして全てのノードが右に子を持つ木が出来上がります。
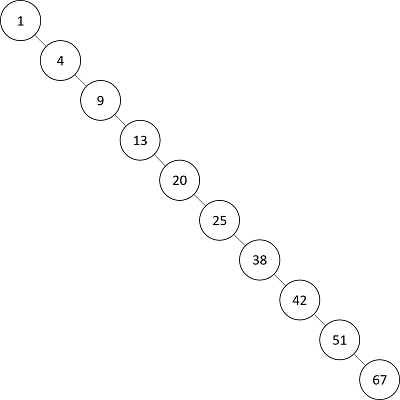
このツリーで67を探索するとルートノードから全てのノードをたどる必要があり、効率的に探索することができません。この場合は最悪$O(n)$の計算量がかかってしまいます。
つまり、効率良い探索を行うためには、木の形が左右に均等に枝分かれしており、きれいな三角形に近い必要があるというわけです。このような効率の良い木を平衡木と呼びます。平衡木は木の高さが$O(\log n)$程度になっています。平衡木にはAVL木、赤黒木、B木など様々な種類がありますが、今回は詳細は省略します。
木の走査
以前学んだリスト構造は一列に並んでいるため、リストの先頭から順番にたどると全てのノードに対して処理することができました。木構造の場合は枝分かれしているため、全てのノードをたどる手順はいくつか考えられます。ここでは木のたどり方について説明します。
木をたどって行くことを木の走査(traverse)と呼びます。まず、各ノードに対して重複しないで1回ずつ処理するために、ルートノードを起点として木を左側からぐるりと巡る一筆書きのようなルートを考えます。
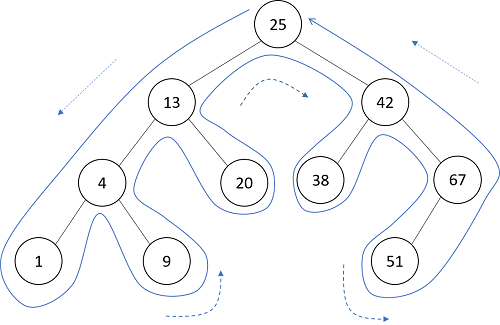
一筆書きといっても各ノードを複数回通っているため、一回ずつ処理するためにはどの通過時点でノードに立ち寄るかを考えなくてはなりません。これには3つの方法があります。
行きがけ順
まず最初に、そのノードを初めて通過した時点で処理するという方法が考えられます。これを行きがけ順(前順、先行順、preorder)といいます。ノードに立ち寄った時点をポイントで表すと次のように図示できます。
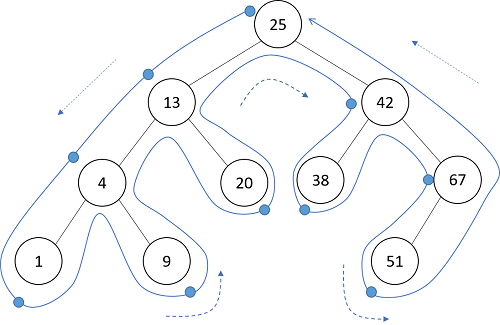
これをプログラミングしてみます。処理としてはノードの値を表示するものとします。前回作った二分探索木のクラスにメソッドprint_preorderとして追加してみましょう。
def print_preorder(self, node):
if node == None:
return
print(node.value, end=" ")
self.print_preorder(node.left)
self.print_preorder(node.right) 引数nodeは通過するノードを表しています。ここでプログラムは再帰関数で表現しています。nodeがNone、つまり木の末端の空ノードに来ればreturnします。行きがけ順なので、最初にprintでノードの値を出力し、次にノードの左(node.left)をたどり、最後に右(node.right)をたどるようにします。
これで先のデータツリーを表示してみましょう。ルートノードからたどるので、ルートを引数に与えます。
tree.print_preorder(tree.root) すると、次のように行きがけ順で出力されます。
25 13 4 1 9 20 42 38 67 51
通りがけ順
次に考えるのは、各ノードの左側をたどった後でそのノードを処理し、それから右側をたどるという順序です。これは通りがけ順(間順、中間順、inorder)と呼ばれます。図で書くと
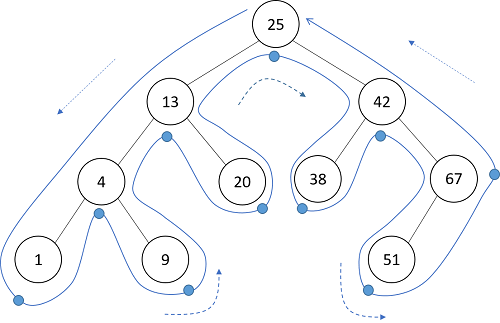
となります。木の末端(例えば①)ノードは左右の子ノードを持たないので、通過時点で処理されます。
プログラムはメソッドprint_inorderとして
def print_inorder(self, node):
if node == None:
return
self.print_inorder(node.left)
print(node.value, end=" ")
self.print_inorder(node.right) と書けます。printの位置が中間に来ています。これも同様に実行すると、
1 4 9 13 20 25 38 42 51 67
となります。
ここで、結果を見るとデータが小さい値から順に整列していることがわかります。つまり、二分探索木を通りがけ順にたどると、ソートされたデータを得ることができます。
帰りがけ順
最後に考えるのは、左側をたどった後、右側をたどり最後にそのノードに立ち寄るという順序です。この方法は帰りがけ順(後順、後行順、postorder)と呼ばれています。
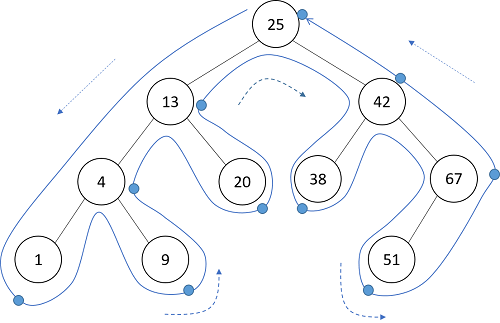
プログラム(print_postorder)も全く同様でprintの位置が最後になっているだけです。
def print_postorder(self, node):
if node == None:
return
self.print_postorder(node.left)
self.print_postorder(node.right)
print(node.value, end=" ") 実行すると、
1 9 4 20 13 38 51 67 42 25
となります。