今回は前回指摘したクイックソートの問題点の改良を行ってみたいと思います。
枢軸の選択
以前お話したように枢軸としてデータの中央値になる要素を選ぶと効率的に処理ができます。前回のプログラムでは右端の要素を枢軸としましたが、この要素の値が中央値に近いかどうかは全く保証されません。かといってデータの中から本当の中央値の要素を見つけるのは、それだけで多くの処理が必要となり本末転倒です。そこで簡単に処理できる方法として
①ランダムにとったいくつかのデータの中から中央値を見つける。
②配列の先頭、中央、末尾の3つのデータから中央値を見つける。
③先頭の2つのデータの中で大きい方をとる。
のようなものが考えられます。とり方は他にもいくらでも考えられますが、次に示すのは②の方法で枢軸を見つけるPythonプログラムの例です。
def med3(a, low, high):
mid = (low + high) // 2
x = a[low]
y = a[mid]
z = a[high]
if (x <= y and y <= z) or (z <= y and y <= x):
swap(a, mid, high)
return y
elif (y <= x and x <= z) or (z <= x and x <= y):
swap(a, low, high)
return x
else:
return z med3関数は、配列aのlowからhighまでの要素のうち、先頭low、中央mid、末尾highの3つの要素からその真ん中の値を返します。このとき、先の分割アルゴリズムが使えるように、その値の要素を末尾highの要素と入れ替えて枢軸としています。
非再帰版クイックソート
またもう一つの問題点として、再帰関数を使うと再帰が深くなりすぎたときに、オーバーフローを起こす可能性があることをあげました。そこで、再帰関数を使わないでクイックソートを書き直してみます。
def quick_sort(a):
stack_low = []
stack_high = []
stack_low.append(0)
stack_high.append(len(a)-1)
while len(stack_low) > 0:
low = stack_low.pop()
high = stack_high.pop()
if low < high:
pos = partition(a, low, high)
if pos - low < high - pos:
stack_low.append(pos+1)
stack_high.append(high)
stack_low.append(low)
stack_high.append(pos-1)
else:
stack_low.append(low)
stack_high.append(pos-1)
stack_low.append(pos+1)
stack_high.append(high) ここでは、再帰関数を使う代わりに、スタックという配列を用意して、そこに分割する範囲の先頭と末尾のlow、highを格納していくことによって、分割する範囲を記憶しておくことにします。
スタック(stack)というのは要素を一つずつ順に入れていき、取り出すときは最後の要素から順に取り出すことができるという入れ物です。箱の中に物を下から順に積み上げて入れていくイメージです。取るときは上から順にとっていきます。
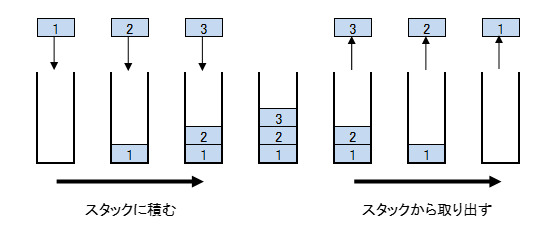
ここでは、lowとhighを入れるスタックstack_low、stack_highを2つ用意します。まず最初に配列aの先頭のインデックス0と末尾len(a)-1をスタックに積みます。Pythonでは配列の末尾に要素を追加するのはappendというメソッドを使います。
それから、スタックが空になるまで、while文で繰り返していきます。while文の最初の処理は、スタックから要素を取り出しています。popが配列の末尾から要素を取り出すメソッドです。これをlow、highとして、lowがhighより小さければ前回と同じpartition関数で分割します。そして、posの左側と右側をスタックに積みます。積まれた分割範囲は次のステップでスタックから取り出され、分割されます。これを繰り返すと分割が進んで行きます。
ここで、分割後スタックに積むときに、if文で何か判定しています。pos-lowはposの左側の要素数、high-posは右側の要素数を表します。すなわち、分割領域の要素数によってスタックに積む順番を変えています。
pos-low(左側)の要素数が少ない場合は、右側→左側の順に積みます。逆に右側の要素数が少ない場合は、左側→右側の順に積みます。スタックは最後から順に取り出されるため、結局左右で要素数が少ない方が先に取り出され処理されることになります。クイックソートは左右の分割された領域は互いに独立しているため、どちらを先に処理しても結果は変わりません。要素数が少ないと分割処理の回数が少なくなるためスタックに積まれる量は少なくなります。そこで、要素数が少ない方を先に処理することで一時的にスタックに積まれている量が少なくなり、スタックのメモリの節約につながります。
この改良を加えたプログラム全体を以下に示しておきます。
def swap(a, i, j):
tmp = a[i]
a[i] = a[j]
a[j] = tmp
def med3(a, low, high):
mid = (low + high) // 2
x = a[low]
y = a[mid]
z = a[high]
if (x <= y and y <= z) or (z <= y and y <= x):
swap(a, mid, high)
return y
elif (y <= x and x <= z) or (z <= x and x <= y):
swap(a, low, high)
return x
else:
return z
def partition(a, low, high):
i = low
j = high - 1
pivot = med3(a, low, high)
while i < j:
while a[i] < pivot:
i += 1
while a[j] >= pivot and j > i:
j -= 1
if i < j:
swap(a, i, j)
if a[i] > pivot:
swap(a, i, high)
return i
def quick_sort(a):
stack_low = []
stack_high = []
stack_low.append(0)
stack_high.append(len(a)-1)
while len(stack_low) > 0:
low = stack_low.pop()
high = stack_high.pop()
if low < high:
pos = partition(a, low, high)
if pos - low < high - pos:
stack_low.append(pos+1)
stack_high.append(high)
stack_low.append(low)
stack_high.append(pos-1)
else:
stack_low.append(low)
stack_high.append(pos-1)
stack_low.append(pos+1)
stack_high.append(high)
a = [82, 78, 3, 91, 15, 12, 59, 40, 24, 63]
print(a)
quick_sort(a)
print(a)ソートの安定性
最後にソートの安定性についてふれておきます。データの中に同じ値の要素が複数あった場合、ソートする前の順番が保たれるようなものを安定なソート(stable sort)と言います。
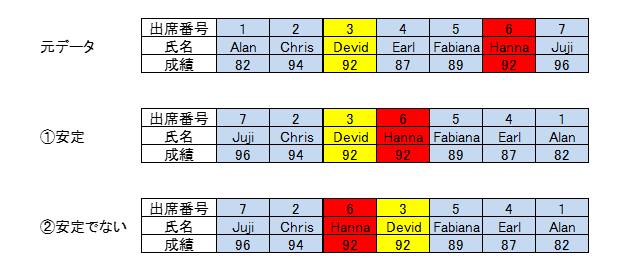
例えば下の図で①は安定なソート、②は安定でないソートとなります。

単純な数値の要素だけを持つデータであれば、同じ数についてソート後の順序はどちらでもよいです。しかし以下の例のように、最初に出席番号順に並んでいた学生を成績順に並べ替えたいとき、同じ成績の場合は出席番号の順番を保つようにしたい場合があります。このときに、安定でないソートを使うと出席番号の順番は保証されなくなります。
これまで見てきたソートの安定性は次のようになっています。
| 選択ソート | 安定でない |
| バブルソート | 安定 |
| クイックソート | 安定でない |
安定でないソートは使えないかというとそうではありません。上記の成績の例で言えば、並べ替え処理の比較に成績と同時に出席番号を含めるとよいです。もし成績が同じ場合は出席番号の大きさを比較するようにすれば、順番が変わらない結果を得ることができます。

