【科学技術計算講座ミニ】ソート（並べ替え）のアルゴリズム② クイックソート

今回はソート（並べ替え）の中でも高速に処理ができるクイックソートについて解説します。

クイックソートとは

選択ソートやバブルソートといったアルゴリズムは計算量が多く、処理速度が遅いというデメリットがありました。

クイックソート（quick sort）は、1960年ごろにC.A.R. Hoareが発表した手法で、高速に並べ替えの処理ができるアルゴリズムです。

基本的には大きなデータを複数の小さなデータに分割して並べ替えを実行していくというコンセプトで、アルゴリズムは以下のようになっています。

①まずデータの中から枢軸（ピボット、pivot）と呼ばれる一つの要素を選択する。
②枢軸より小さな要素は右側に、大きな要素は左側に集める（分割）。
③②の右側（小さな要素）と左側（大きな要素）でそれぞれ分割処理を繰り返す。
④各分割要素が一つになるまで繰り返す。

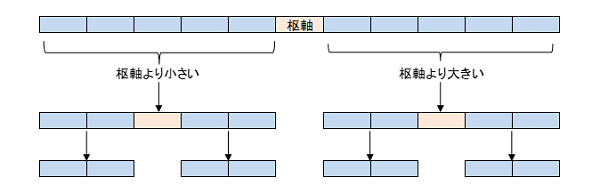
このようにクイックソートは、大きな問題を直接扱うのではなく、小さな問題に分割して処理していくという分割統治法と呼ばれる手法の一種になります。

また、クイックソートの平均的な計算量は$O(n \log n)$です。

クイックソートの分割

クイックソートのメイン部分はどのようにデータを分割するか（上記②）というところです。ここでは分割のアルゴリズムを説明します。

その前に枢軸をどう選ぶかというのが問題となりますが、ここでは配列データの右端（最後の要素）を枢軸とすることにします。枢軸は任意にとれるので、もちろん他の要素でも構いませんが、以下の手順では右端に枢軸があるものとして処理しています。

①インデックスiをデータの先頭から右に向かって、枢軸より大きな要素の所まで進めていく。（下図(1)）
②インデックスjを枢軸の一つ手前の要素から左に向かって、枢軸より小さな要素の所まで進めていく。（下図(1)）
③iとjの要素を入れ替える。（下図(2)）
④iとjが交差するまで繰り返す。（下図(3)(4)）
⑤iと枢軸の要素を入れ替える。（下図(5)）

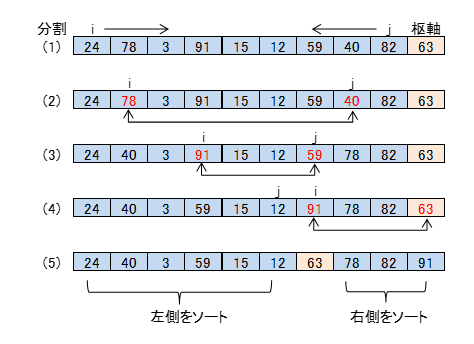
このようにすると、最終的に枢軸の左側に枢軸より小さな要素、右側に大きな要素が集まっていることがわかります。あとは、左側と右側で同じ分割を繰り返して行きます。

クイックソートのプログラム

では、クイックソートのプログラム例をPythonで示しておきます。

def swap(a, i, j):
  tmp = a[i]
  a[i] = a[j]
  a[j] = tmp

def partition(a, low, high):
  i = low
  j = high - 1
  pivot = a[high]

  while i < j:
    while a[i] < pivot:
      i += 1
    while a[j] >= pivot and j > i:
      j -= 1
    if i < j:
      swap(a, i, j) 

  if a[i] > pivot:
    swap(a, i, high)

  return i

def quick_sort(a, low, high):
  if low >= high:
    return
  pos = partition(a, low, high)
  quick_sort(a, low, pos-1)
  quick_sort(a, pos+1, high)

a = [82, 78, 3, 91, 15, 12, 59, 40, 24, 63]
print(a)
quick_sort(a, 0, len(a)-1)
print(a)

swap関数は選択ソートのときに説明した配列要素を入れ替える関数です。

partition関数は配列データaを分割するための関数です。low、highはデータの中で分割しようとする最初と最後のインデックスを表しています。ここで枢軸pivotは右端にあるのでa[high]の要素を代入しています。

最初のwhile文でiがjより小さい間は処理を繰り返します。処理は、a[i]がpivot以上になるまでiを進め、同様にa[j]がpivotより小さくなるまでjを進め、要素を入れ替えていきます。

最後、a[i]とpivotの要素a[high]を入れ替えて、その時のiを返します。

クイックソートのメイン関数はquick_sort関数です。これは再帰関数を使って書くとかなり簡単に書くことができます。最初のif文はソートの停止条件でlowとhighが一致する（分割要素が一つ）か逆転したら何も処理をしないで返します。

次にpartition関数を呼んで分割し、枢軸のインデックスをposとします。そして、posの左側（low～pos-1）と右側（pos+1～high）を再帰関数で呼び出しソートを繰り返します。

クイックソートの問題点

ここで示したクイックソートのアルゴリズムにはいくつか問題点があることが指摘されています。

まず枢軸の選び方です。クイックソートでは枢軸としてデータの中央値（データを整列したときにちょうど真ん中にくる値）の要素を選ぶと効率的に分割処理が進みます。ところが、すでにきれいに並んでいるようなデータを考えた場合、その中で最も大きな値を枢軸にとると、分割しても左側に全てのデータが集まってしまい、分割処理をデータ数分繰り返し続けなくてはなりません（下図）。この場合最悪$O(n^2)$の計算量になってしまいます。

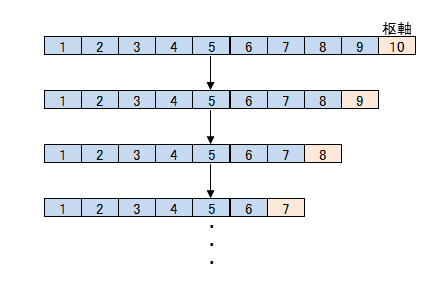
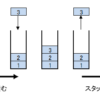
またこの状態は、再帰処理の深さに関係します。データ量が多かったり、上記のように何度も再帰処理が実行されるような状態になると、スタックオーバーフローといってメモリ領域が足りなくなり、プログラムがエラーで停止することがあります。

クイックソートを少ないメモリや計算量で効率的に実行するためにプログラムやアルゴリズムを改善していく必要があります。詳細は以下の講座でお話したいと思います。

全体の目次