【科学技術計算講座5-9】SPH法～粒子にかかる力の計算

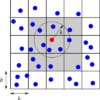
前回は近傍粒子の探索方法についてお話しました。

今回からナビエ＝ストークス方程式の解き方に入っていきます。まず、粒子にかかる力の計算についてお話します。

粒子にかかる力

粒子の運動方程式は次式のナビエ＝ストークス方程式で表されます。

$$\frac{D {\bf v}}{D t} = -\frac{1}{\rho} \nabla p + \frac{\mu}{\rho} \nabla^2 {\bf v} + {\bf g} \tag{9-1}$$

右辺は、それぞれ圧力項、粘性項、外力項という力の項を表しています。

微分項の離散化

(9-1)式の右辺には微分の形がでてきます。SPH法では微分項はどのように離散化されるのでしょうか。【5-6】章の(6-1)式より、物理量$\phi$の勾配は、

$$\nabla \phi({\bf r}) = \int \nabla_{r'} \phi({\bf r}') W({\bf r}-{\bf r}') dV \tag{9-2}$$

と表されます。ここで、積の微分により、

$$\int \nabla_{r'} (\phi({\bf r}') W({\bf r}-{\bf r}')) dV = \int \nabla_{r'} \phi({\bf r}') W({\bf r}-{\bf r}') dV + \int \phi({\bf r}') \nabla_{r'} W({\bf r}-{\bf r}') dV \tag{9-3}$$

なので、(9-2)式は、

$$\nabla \phi({\bf r}) = \int \nabla_{r'} (\phi({\bf r}') W({\bf r}-{\bf r}')) dV - \int \phi({\bf r}') \nabla_{r'} W({\bf r}-{\bf r}') dV \tag{9-4}$$

と変形できます。ここで、(9-4)式の右辺第一項はガウスの発散定理より

$$\int \nabla_{r'} (\phi({\bf r}') W({\bf r}-{\bf r}')) dV = \int_S \phi({\bf r}') W({\bf r}-{\bf r}') dS \tag{9-5}$$

なのですが、カーネル関数$W$の端部は０なので、この項は０となり、最終的に

$$\nabla \phi({\bf r}) = \int \phi({\bf r}') \nabla_{r} W({\bf r}-{\bf r}') dV \tag{9-6}$$

と表せます（カーネル関数は【5-6】章で見たように原点を中心に左右対称の偶関数なので、勾配は２つの粒子間では大きさは同じで符号が逆という性質を使って符号を変えています）。これも、(6-2)式と同様に離散形式で表すと、

$$\nabla \phi({\bf r}_i) = \sum_j \frac{m_j}{\rho_j} \phi({\bf r}_j) \nabla W({\bf r}_i-{\bf r}_j) \tag{9-7}$$

となり、物理量の勾配はカーネル関数の勾配を用いて表すことができます。

圧力項

さてこれを用いると、(9-1)式の圧力項は、

$$-\frac{1}{\rho} \nabla p = -\frac{1}{\rho_i} \sum_j \frac{m_j}{\rho_j} p_j \nabla W({\bf r}_i-{\bf r}_j) \tag{9-8}$$

と書くことができます。ところが、この離散式をよく見ると、粒子$i$の圧力$p_i$と粒子$j$の圧力$p_j$が異なるため、$i$から$j$を見たときの力と、$j$から$i$を見たときの力が一致しないことがわかります。これは、作用反作用の法則に反することになります。つまり、離散式として２つの粒子に働く力は、大きさが同じで向きが逆の反対称性を持つ必要があります。

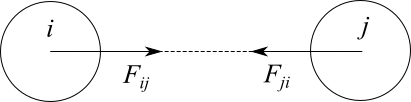
そこで、以下の関係

$$\nabla \left( \frac{p}{\rho} \right) = \frac{\nabla p}{\rho} - \frac{p}{\rho^2} \nabla \rho \tag{9-9}$$

を使って圧力項を書き直すと、

$$-\frac{1}{\rho} \nabla p = -\left( \nabla \left( \frac{p}{\rho} \right) + \frac{p}{\rho^2} \nabla \rho \right) \tag{9-10}$$

となります。この右辺に対して(9-7)式の離散化を行うと、

$$\begin{split} -\frac{1}{\rho} \nabla p &= -\left( \sum_j \frac{m_j}{\rho_j} \left( \frac{p_j}{\rho_j} \right) \nabla W({\bf r}_i-{\bf r}_j) + \frac{p_i}{\rho_i^2} \sum_j \frac{m_j}{\rho_j} \rho_j \nabla W({\bf r}_i-{\bf r}_j) \right)\\ &= - \sum_j m_j \left( \frac{p_j}{\rho_j^2} + \frac{p_i}{\rho_i^2} \right) \nabla W({\bf r}_i-{\bf r}_j) \end{split} \tag{9-11}$$

と書くことができます。これで、$i$、$j$相互に見たときに反対称性が保たれた離散式ができあがりました。

粘性項

次に粘性項ですが、こちらも同様に離散化することができ、様々な定式化が考えられています。ここでは文献[1][2]に従い

$$\frac{\mu}{\rho} \nabla^2 {\bf v} = \sum_j m_j \frac{\mu_i + \mu_j}{\rho_i \rho_j} \frac{({\bf r}_i-{\bf r}_j) \cdot \nabla W({\bf r}_i-{\bf r}_j)}{|{\bf r}_i-{\bf r}_j|^2 + \eta^2} ({\bf v}_i - {\bf v}_j) \tag{9-12}$$

ここで、$\eta^2 = 0.01 h^2$

の離散式を使うことにします。

この定式化も反対称性を持ち、２階微分がカーネル関数の勾配を使って表されています。

外力項

重力の項は単純に重力加速度を与えるだけです。

プログラミング

では粒子にかかる力の計算をJavaScriptでプログラミングしてみましょう。力の計算部分はparticleForceという関数にします。

function particleForce() {
  for (let i = 0, n = p.length; i < n; i++) {
    if (!p[i].active) continue;

    let force = new Vector();

    p[i].forNeighbor(cell, function(pNeighbor, rv) {
      if (p[i] !== pNeighbor) {
        const r = rv.magnitude();

        // pressure force
        const wp = w.gradient(rv);
        const fp = -massParticle
          * (pNeighbor.pressure / (pNeighbor.density * pNeighbor.density)
          + p[i].pressure / (p[i].density * p[i].density));
        force.x += wp.x * fp;
        force.y += wp.y * fp;

        // viscosity force
        const r2 = r * r + 0.01 * h * h;
        const dv = p[i].velocity.sub(pNeighbor.velocity);
        const fv = massParticle * 2 * viscosity / (pNeighbor.density * p[i].density) * rv.dot(wp) / r2;
        force.x += fv * dv.x;
        force.y += fv * dv.y;
      }
    });

    // gravity force
    force.x += grv.x;
    force.y += grv.y;

    // update
    p[i].force.x = force.x;
    p[i].force.y = force.y;
  }
}

力はすべての流体粒子に対して求めるので最初にforループで回します。

    let force = new Vector();

    p[i].forNeighbor(cell, function(pNeighbor, rv) {
       if (p[i] !== pNeighbor) {

forceは力を表しベクトルとして定義します。p[i].forNeighborで粒子$i$の近傍粒子に対してループして力の和を求めます。if (p[i] !== pNeighbor) のif文は粒子$i$と異なる粒子のみ処理するためです。

        // pressure force
        const wp = w.gradient(rv);
        const fp = -massParticle
          * (pNeighbor.pressure / (pNeighbor.density * pNeighbor.density)
          + p[i].pressure / (p[i].density * p[i].density));
        force.x += wp.x * fp;
        force.y += wp.y * fp;

まず、(9-11)式より圧力項を計算します。w.gradient(rv)でカーネル関数の勾配をとっています。力はforceのx、yプロパティに加えていきます。

        // viscosity force
        const r2 = r * r + 0.01 * h * h;
        const dv = p[i].velocity.sub(pNeighbor.velocity);
        const fv = massParticle * 2 * viscosity / (pNeighbor.density * p[i].density) * rv.dot(wp) / r2;
        force.x += fv * dv.x;
        force.y += fv * dv.y;

次に(9-12)式より粘性項を計算します。粘性係数viscosityはすべての粒子で一定として２倍しています。

    // gravity force
    force.x += grv.x;
    force.y += grv.y;

    // update
    p[i].force.x = force.x;
    p[i].force.y = force.y;

最後に重力加速度ベクトル（grv）を加え、粒子オブジェクトのforceプロパティに代入しています。

まとめ

ナビエ＝ストークス方程式に出てくる粒子にかかる力の計算方法について説明しました。離散化の仕方はここにあげた以外にも多くの定式化が考えられています。

これで力が求まったので、次回はナビエ＝ストークス方程式を数値的に解く方法についてお話したいと思います。

参考文献

[1] Morris, J. P.; Fox, P. J.; Zhu, Y. Modeling low Reynolds number incompressible flows using SPH. J. Comput. Phys. 1997, vol. 136, p. 214-226.

[2] Lee, E.-S.; Moulinec, C.; Xu, R. et al. Comparisons of weakly compressible and truly incompressible algorithms for the SPH mesh free particle method. J. Comput. Phys. 2008, vol. 227, p. 8417-8436.

←前回　近傍粒子の探索
 →次回　Leap-Frog法で運動方程式を解く

全体の目次