前回はSPH法の密度・圧力の計算方法についてお話しました。
今回はSPH法で近傍粒子をどのように見つけるかについて説明します。
目次
近傍粒子に対する和
前回、SPH法で密度を計算するために次の定式化を行いました。
$$\rho_i = \sum_j m_j W({\bf r}_i-{\bf r}_j) \tag{8-1}$$
この式は、粒子$i$の場所の密度を求めるためには、その周りにあるすべての粒子$j$に対する和を計算する必要があることを示しています。
一方で、カーネル関数$W$は、影響半径$h$より遠い場所ではゼロになるので結局、半径$h$より内側の粒子に対して和をとるだけでよいことがわかります。
しかし、周りの粒子が$h$より近いかどうかを判定するためには、結局すべての粒子$j$に対してその粒子との距離を判定しなくてはなりません。密度はすべての粒子$i$について計算するため、この判定操作を全粒子で行います。プログラムで書くと次のようになります。
for (let i = 0, n = p.length; i < n; i++) {
for (let j = 0, n = p.length; j < n; j++) {
// p[i]とp[j]の距離がhより小さいかどうかを判定
// 距離が近れば和を計算
}
}forループの中にforループがあり二重になっています。例えば粒子が全部で10個あるとすると、全体の計算量は10×10=100回になります。100回程度だと大した計算量ではありませんが、粒子数が100個あると1万回、1000個あると100万回、1万個の粒子だと1億回というように、Nの2乗で計算量が増えていきます。つまり、SPH法で最も計算時間がかかるのは、この近傍粒子を探索する部分になるのです。
そこで、近傍粒子を見つけるために、何か工夫をして計算量を減らしてやる必要があります。ここでは、その一例を紹介します。
空間分割法
近傍粒子の探索方法
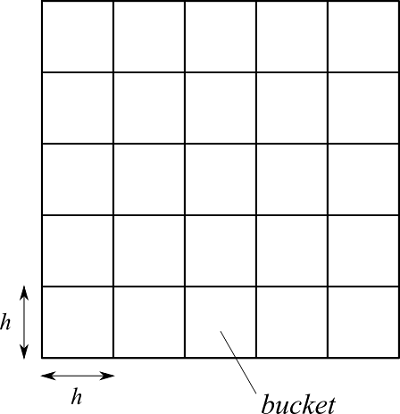
まず計算領域を格子状に分割します。このとき、格子幅は影響半径$h$とします。分割された格子をバケット(bucket)と呼びます(バケツです)。
粒子がこの空間上に配置されているとします。ある粒子$i$の周りの粒子を探索する場合には、粒子$i$が位置しているバケットとそれに隣接するバケット(下図の灰色)に位置している粒子$j$のみで距離判定を行います。
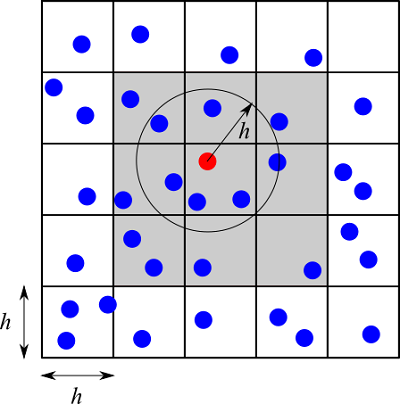
格子幅が$h$なので、上記範囲のさらに外側のバケットにいる粒子との距離は必ず$h$より大きくなるため、この範囲内の粒子のみで距離判定を行えば十分です。
所属するバケット
この方法では、粒子がどのバケットに属しているかを見つける必要があります。これは簡単に計算できます。
下図のように領域の左下角を原点とした空間分割を考えます。原点を0としてバケットに対して、x方向とy方向にインデックス番号$I_x$、$I_y$をふります。
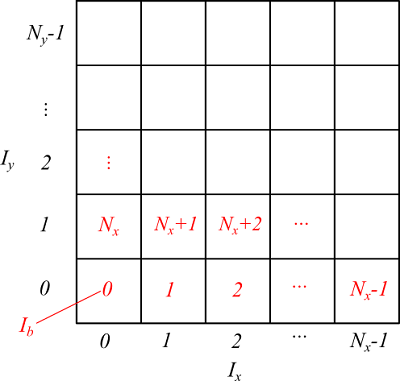
このとき、インデックス $(I_x, I_y)$ のバケット番号を
$$I_b = I_x + I_y \times N_x \tag{8-2}$$
ここで、$N_x$はx方向の分割数
と定義します。こうすると、左下角のバケットを0番として順番にバケットに通し番号をつけることができます。
いま、粒子が$(x, y)$の位置にいるとき、その場所のインデックス$(I_x, I_y)$は、
$$I_x = \left\lfloor \frac{x}{h} \right\rfloor$$
$$I_y = \left\lfloor \frac{y}{h} \right\rfloor \tag{8-3}$$
で求まります。$ \lfloor a \rfloor$は、$a$以下の最大の整数を表します。この場合は、$x$を$h$で割った商と同じです。あとは、(8-2)式よりバケットの通し番号がすぐに計算できます。
この方法を使うと、すべての粒子に対してループを1回まわすだけで、その粒子がどのバケットに属しているかを決めることができます。
近傍粒子の探索
近傍粒子の探索の際は、対象となる粒子$i$の座標$(x, y)$から同様にバケット番号を求めます。そして、そのバケットに隣接する9つのバケットに属している粒子に対してループを回して、粒子$i$との距離を計算し、$h$より近くにある粒子のみ処理していきます。
こうすることで、すべての粒子に対して判定をすることなく、効率的に近傍粒子を見つけることができます。
プログラム
ではJavaScriptでプログラミングしてみましょう。
空間分割法のクラス
空間分割法のためのクラスを作ります。クラス名はCellとしておきます。
class Cell {
constructor(region, h) {
this.h = h;
this.nx = Math.ceil(region.width / this.h);
this.ny = Math.ceil(region.height / this.h);
this.bucket = new Array(this.nx * this.ny);
this.region = region;
}
clear() {
for (let i = 0, n = this.bucket.length; i < n; i++) {
this.bucket[i] = [];
}
}
add(p) {
for (let i = 0, n = p.length; i < n; i++) {
if (!p[i].active) continue;
this.bucket[p[i].indexCell(this)].push(p[i]);
}
}
}コンストラクター
コンストラクターの引数は、regionとhです。regionはまた後でお話しますが、矩形の領域を表すオブジェクトで、計算領域を示しています。hは影響半径です。
プロパティにはまず、影響半径h、x方向分割数nx、y方向分割数nyをセットしています。regionのwidth、heightは矩形領域のx方向とy方向の幅です。Math.ceilは小数を切り上げて整数にするという数学関数なので、領域の幅をhで割って分割数を求めています。
次のbucketは分割されたバケットを表します。バケットは$N_x \times N_y$個の要素を持つ配列として定義しています。
最後のregionは、領域の大きさなどを残しておくためにregionオブジェクトを代入しています。
バケットのデータ構造
ここで、bucketについて説明します。bucketは配列ですが、その要素一つ一つが一つのバケット(格子)を意味しています。配列のインデックスはバケット番号(8-2)式を表します。そして、bucket要素もまた、それぞれを配列として定義し、そこに属する粒子オブジェクトを格納していきます。
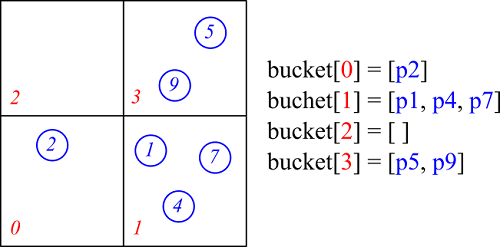
this.bucket[バケット番号] = [粒子0、粒子1,粒子2、...]
つまり、bucketは2次元配列のようなデータ構造をしています。
メソッド
メソッドは、add、clearという2つを用意します。
clearは、バケットを空にするメソッドです。
一方、addはバケットに粒子を格納していくメソッドです。引数には粒子オブジェクトの配列をとります。ここで、p[i].indexCell(this)は、その粒子が属するバケット番号を表します(次の項で詳しく説明します)。addメソッドでは、すべての粒子に対して、その粒子が属するバケットの配列に追加するという操作を行っています。
粒子のクラス
粒子クラス(class Particle)は前回作成しましたが、近傍粒子探索のためのメソッドをいくつか追加しておきましょう。
インデックスのメソッド
indexX(cell) {
return Math.floor((this.position.x - cell.region.left) / cell.h);
}
indexY(cell) {
return Math.floor((this.position.y - cell.region.bottom) / cell.h);
}
indexCell(cell) {
return this.indexX(cell) + this.indexY(cell) * cell.nx;
}まずは、その粒子がどのバケットに属するかを表すインデックスを返すメソッドです。
indexX、indexYは、(8-3)式から粒子の場所のインデックス$I_x$、$I_y$を返します。引数のcellは前項の空間分割オブジェクトです。cell.region.leftは領域の左端のx座標、cell.region.bottomは下端のy座標を表しています(左下角を原点として計算)。
indexCellは、(8-2)式のバケット番号を返しています。
近傍粒子のループメソッド
forNeighbor(cell, func) {
const indexX = this.indexX(cell);
const indexY = this.indexY(cell);
for (let i = indexX-1; i <= indexX+1; i++) {
if (i < 0 || i >= cell.nx) continue;
for (let j = indexY-1; j <= indexY+1; j++) {
if (j < 0 || j >= cell.ny) continue;
const indexCell = i + j * cell.nx;
for (let k = 0, n = cell.bucket[indexCell].length; k < n; k++) {
const pNeighbor = cell.bucket[indexCell][k];
const rv = this.position.sub(pNeighbor.position);
if (rv.magnitude() >= cell.h) continue;
func(pNeighbor, rv);
}
}
}
}そして前回、密度計算のプログラムで出てきましたが、近傍粒子に対してループするメソッドforNeighborを作成します。このメソッドには、ある粒子(自分、this)の周りのバケットに属する粒子に対して、ループして処理する操作を定義します。
const indexX = this.indexX(cell);
const indexY = this.indexY(cell);まず、自分が属するバケットのインデックス$I_x$、$I_y$を計算します。
for (let i = indexX-1; i <= indexX+1; i++) {
if (i < 0 || i >= cell.nx) continue;
for (let j = indexY-1; j <= indexY+1; j++) {
if (j < 0 || j >= cell.ny) continue;
const indexCell = i + j * cell.nx;そして、自分のバケットに隣接するバケット($I_x-1 \sim I_x+1$、$I_y-1 \sim I_y+1$のインデックスを持つ)に対してループします。if文はインデックスが領域から外れるとスキップするようにしています。そして、バケット番号を求めてindexCellとします。
for (let k = 0, n = cell.bucket[indexCell].length; k < n; k++) {
const pNeighbor = cell.bucket[indexCell][k];
const rv = this.position.sub(pNeighbor.position);
if (rv.magnitude() >= cell.h) continue;
func(pNeighbor, rv);
}求まったバケット番号に属している粒子に対してループする部分です。pNeighborに近傍粒子のオブジェクトが入ります。rvは、自分の位置から近傍粒子の位置を引いた距離ベクトルが計算されます。if文では、距離が影響半径$h$以上であればスキップするようにしています。
最後のfuncは関数なのですが、forNeighborの引数になっています。これは前回密度計算のときに示した
p[i].forNeighbor(cell, function(pNeighbor, rv) {
const r = rv.magnitude();
density += w.kernel(r) * massParticle;
});のfunction(pNeighbor, rv) {...} という関数を表しています。つまり、上記funcには「実際にforNeighborメソッドを使うところで定義する関数」が入力され実行されるというわけです。
以上が、今回使用する近傍粒子の探索法ですが、他にも四分木や八分木といった木構造による空間分割法もあります。また、データ構造やアルゴリズムもメモリや計算速度の観点から色々考えられています。このあたりは色々調べてみると面白いです。
まとめ
SPH法における近傍粒子の探索方法について解説しました。内容は少しややこしかったかも知れませんが、粒子法を考える上で近傍粒子の探索は重要な部分になります。プログラムも徐々に出来てきました。
次回はいよいよナビエ=ストークス方程式を解く段階に入っていきたいと思います。