【科学技術計算講座5-6】SPH法の離散化

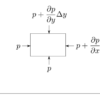
前回はSPH法の基礎方程式であるナビエ＝ストークス方程式と連続の式を導出し解説しました。

今回からSPH法の具体的手法に入っていきます。まず初めにSPH法の離散化の方法について説明します。

SPH法の離散化

前回、流体の基礎方程式をたてたので、これを解いていくと流れの様子が求まります。以前の講座で行ったように、格子法では空間を微小な領域に分割し、それぞれの微小領域に対し差分法や有限体積法による離散化で基礎方程式を解いていきました。粒子法では流体を流体粒子で表します。粒子１個１個の運動を計算することで、流体全体の挙動を計算します。この場合、粒子１個１個を計算点とみなし、離散化を行っていきます。

ここで、粒子というのは必ずしも球（２次元だと円）形をしているわけではありません。可視化や図の説明ではイメージしやすいように円形に描いていますが、これは便宜上そういうふうに図示しているだけで、具体的な形状を持っているわけではありません。あくまで仮想的な粒子です。ただし、粒子は質量と大きさを持っています。あと、粒子の位置や速度といった情報も持っています。

このような粒子で考えると、以前の講座でやった惑星の運動の計算に似ています。ただし、大きく違うのは流体粒子の場合は、１個１個が完全に独立しているのではなく、粒子全体として流体の挙動を表す必要があるということです。ここではそれを表すための粒子法の離散化を見ていきましょう。

積分形式

粒子法では、ある物理量$\phi({\bf r})$を表す場合、

$$\phi({\bf r}) = \int \phi({\bf r}') W({\bf r}-{\bf r}') dV \tag{6-1}$$

という積分形で記述します。これは、位置${\bf r}$の物理量$\phi$は、その周辺の物理量に重み関数$W$を掛けて体積積分したものである、という意味になります。

重み関数

ここで、重み関数$W$は下図のような釣鐘型の形をしています。

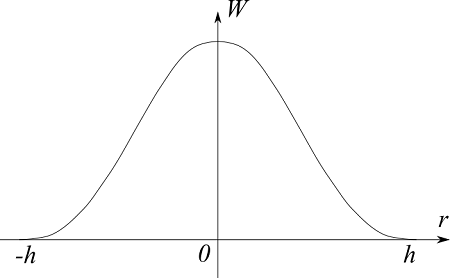
これは、物理量を計算するときに中心付近ほど影響度合いが大きく、遠ざかるにつれて影響が小さくなることを意味しています。さらに、距離$h$より離れると関数はゼロとなり全く影響を及ぼさなくなります。この$h$のことを影響半径と呼びます。

また、詳しくは省略しますが、重み関数$W$は積分すると１になったり、他にも数学的にいくつかの性質を持っています。このような重み関数をカーネル（kernel）関数と呼んでいます。

離散形式

粒子法では粒子で離散化するため、粒子$i$の位置での物理量$\phi({\bf r}_i)$を計算する場合、(6-1)式を次のように周辺粒子$j$の和として表します。

$$\phi({\bf r}_i) = \sum_j \frac{m_j}{\rho_j} \phi({\bf r}_j) W({\bf r}_i-{\bf r}_j) \tag{6-2}$$

ここで、$m_j$、$\rho_j$はそれぞれ粒子$j$の質量、密度で、体積$dV_j = m_j / \rho_j$より上式となっています。

つまり、影響半径$h$内にある粒子がその中心での物理量を決めるという形式をとっています。

カーネル関数

ここではカーネル関数の具体的な形を見てみましょう。カーネル関数は必要な性質を満たせば任意にとることができます。実際、様々なカーネル関数が提唱されています。ここではPoly6と呼ばれるカーネル関数[1]を使うことにします。

Poly6カーネル関数

Poly6カーネル関数は、次のように$r$の6次式で表されます。

$$W({\bf r}) = \begin{equation} \begin{cases} \; \alpha ( h^2 - r^2)^3 & r<h \\ \; 0 & r \ge h \end{cases} \end{equation} \tag{6-3}$$

ここで、２次元では$\alpha = 4 / (\pi h^8)$、３次元では$\alpha = 315 / (64 \pi h^9)$。

また、後で出てきますが勾配が必要になるので、関数の勾配も求めておきます。

$$\nabla W({\bf r}) = \begin{equation} \begin{cases} \; -6 \alpha ( h^2 - r^2)^2 {\bf r} & r<h \\ \; 0 & r \ge h \end{cases} \end{equation} \tag{6-4}$$

プログラミング

カーネル関数の具体的な式を決めたので、JavaScriptでプログラミングしてみましょう。【5-4】章で説明したオブジェクト指向のクラスを用いてカーネル関数クラスを作っておきます。

class Kernel {
  // Poly6 kernel
  constructor(h) {
    this.h = h;
    this.alpha = 4 / (Math.PI * Math.pow(h, 8));
  }

  kernel(r) {
    if (r < this.h) {
      return this.alpha * Math.pow(this.h * this.h - r * r, 3);
    } else {
      return 0;
    }
  }
  
  gradient(rv) {
    const r = rv.magnitude();
    if (r < this.h) {
      const c = -6 * this.alpha * Math.pow(this.h * this.h - r * r, 2);
      return new Vector(c * rv.x, c * rv.y);
    } else {
      return new Vector();
    }
  }
}

クラスの名前はKernelとします。コンストラクターは、影響半径hを引数として、$h$と$\alpha$をプロパティにしています（ここでは２次元を考えます）。

次に、カーネル関数を計算するメソッドkernelを定義します。引数は、中心からの距離rで、(6-3)式で与えられる値を返しています。

そして、勾配を計算するgradientメソッドを定義します。勾配はベクトルなので、引数には距離ベクトルrvを入力します。rvは以前作成したベクトルクラスのオブジェクトで、メソッドmagnitude()で大きさを計算してrとしています。最終的に(6-4)式で計算されたベクトルを返しています。

このクラスを使って、プログラム内で、

let w = new Kernel(h);

としてやると、変数wにカーネル関数のオブジェクトが定義できます。

まとめ

SPH法の離散化とカーネル関数についてお話しました。カーネル関数を使うなど、格子法の差分形式とはずいぶん違う離散化になっています。

次回は密度や圧力といった物理量をどう表すかについて説明したいと思います。

参考文献

[1] Müller, M.; Charypar, D.; Gross, M. Particle-Based Fluid Simulation for Interactive Applications. In Proc. of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer
Animation. 2003, p. 154–159.

←前回　ナビエ=ストークス方程式の導出
 →次回　SPH法の密度、圧力

全体の目次