【科学技術計算講座5-11】初期条件と境界条件

前回は粒子の運動方程式を数値的に解くLeap-Frog法について説明しました。

今回は初期条件と境界条件についてお話します。

計算領域

空間を扱う数値計算をするためには、計算領域を決めておく必要があります。無限の遠方まで計算することはできないので、どこか適当な領域を決めて、その内部で計算を行っていきます。

ここでは、次のような２次元の領域を考えましょう。

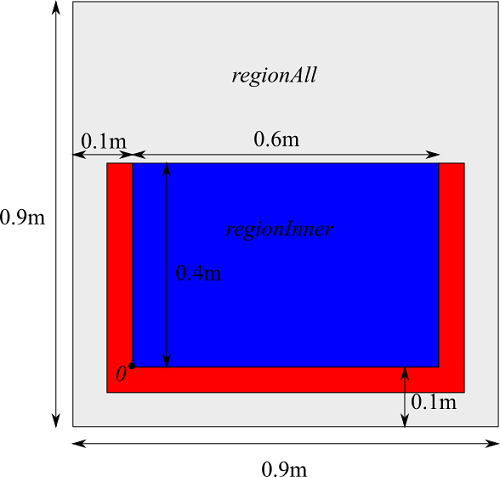
全体の計算領域は0.9m×0.9mの矩形で、regionAllと名付けることにします。その中に水槽が置かれています。水槽は内側の左下角を原点とし、幅0.6m×高さ0.4mのサイズです。この水槽の内側はregionInnerとします。水槽はある厚みを持っていますが、これは後ほど説明します。

領域のクラス

ここでは２次元を扱いますが、領域はすべて矩形で表すことができるものとします。そこで、矩形の領域を表すオブジェクトを作っておくと後々プログラムしやすいです。

class Rectangle {
  constructor(x, y, width, height) {
    this.width = width;
    this.height = height;
    this.left = x;
    this.right = x + width;
    this.bottom = y;
    this.top = y + height;
  }
}

矩形の領域を表すクラスRectangleを作ります。コンストラクターは、左下角の座標x、yと幅width、高さheightを引数にとります。プロパティのleftは左端のx座標、rightは右端のx座標、bottomは下端のy座標、topは上端のy座標を表します。

パラメータの入力

ここでは、講座の最初で示したダム崩壊の計算を考えます。まず計算に必要な条件やパラメータを指定する関数を用意しておきます。setParameter関数を作ります。

function setParameter() {
  // particle
  particleSize = 0.01;
  h = particleSize * 1.5;
  stiffness = 100;
  density0 = 1000;
  viscosity = 1;
  massParticle = particleSize * particleSize * density0;
  w = new Kernel(h);
  grv = new Vector(0, -9.8);

  // region
  regionAll = new Rectangle(-0.1, -0.1, 0.8, 0.8);
  regionInner = new Rectangle(0, 0, 0.6, 0.4);
  regionInitial = new Rectangle(0, 0, 0.2, 0.4);
  thicknessWall = particleSize * 4;
  cell = new Cell(regionAll, h);

  // time
  timeDelta = 0.001;

  // canvas
  canvasWidth = 600;
  canvasHeight = canvasWidth * regionAll.height / regionAll.width;
}

particleSizeは、粒子の大きさで、ここでは0.01mとします。小さくすると多くの粒子を定義することになります。
hは、影響半径で粒子サイズの1.5倍としておきます。（必ずしもこの値というわけではないので、変えてみて影響度合いを確かめてみるとよいでしょう。）
stiffnessは、圧力の剛性$k$です（【5-7】章の(7-5)式）。
density0は、同じ圧力の式に出てくる基準密度$\rho_0$です。
viscosityは、粘性係数$\mu$を表します（【5-9】章の(9-12)式）。（安定に計算するために、粘性係数は大きめに設定しています。）
massParticleは、粒子の質量$m$です。
wは、カーネル関数のオブジェクト。
grvは、重力加速度ベクトル${\bf g}$で、y方向鉛直下向きにかかっています。

次のregionは領域を表すオブジェクトで、regionAll（領域全体）、regionInner（水槽内部領域）、regionInitial（水の初期位置）を定義しています。

thicknessWallは、水槽の壁の厚みを表し、粒子サイズの４倍とします。この計算では後述するように、水槽の壁も粒子でモデル化しています。つまり、壁は粒子が４個分の厚みになっています。cellは、空間分割のオブジェクトです（【5-8】章）。

timeDeltaは、時間刻み$\Delta t$で、ここでは0.001秒としています。

最後のcanvasWidth、canvasHeightは可視化のキャンバスの大きさを指定して、横幅が600pxになるようにしています。

なお、これらの変数はletで宣言していませんが、これはグローバル変数（関数の外で宣言する変数）として定義しています。グローバル変数はどの関数の中でも参照できます。

初期条件

次に、粒子の初期条件を考えます。ダム崩壊問題では水槽内の一部に水柱が位置している条件です。この領域は前述のregionInitialで設定しています。あと、今回は水槽の壁も粒子で表すため、その場所にも粒子を配置する必要があります。

では、粒子の初期配置を設定するJavaScriptプログラムを作ります。関数名はinitialParticleとします。

function initialParticle() {
  const create = function(p, region) {
    const nx = Math.round(region.width / particleSize);
    const ny = Math.round(region.height / particleSize);

    for (let i = 0; i < nx; i++) {
      for (let j = 0; j < ny; j++) {
        const x = region.left + (i + 0.5) * particleSize;
        const y = region.bottom + (j + 0.5) * particleSize;
        p.push(new Particle(x, y));
      }
    }
  };

  // fluid particle
  p = [];
  create(p, regionInitial);

  // wall particle
  pWall = [];
  const width = regionInner.width + 2 * thicknessWall;
  const regionWallBottom = new Rectangle(-thicknessWall, -thicknessWall, width, thicknessWall);
  create(pWall, regionWallBottom);

  const regionWallLeft = new Rectangle(-thicknessWall, 0, thicknessWall, regionInner.height);
  create(pWall, regionWallLeft);

  const regionWallRight = new Rectangle(regionInner.right, 0, thicknessWall, regionInner.height);
  create(pWall, regionWallRight);
}

  const create = function(p, region) {

最初のcreateは、粒子を領域に配置する関数です。粒子配列pと領域regionを引数に入れると、粒子の位置を計算してp配列に粒子オブジェクトを定義していきます。粒子は矩形に順に並ぶよう配置しています。

  // fluid particle
  p = [];
  create(p, regionInitial);

pは流体粒子を表す配列で、先程のcreate関数で、初期領域regionInitialに配置しています。

  // wall particle
  pWall = [];
  const width = regionInner.width + 2 * thicknessWall;
  const regionWallBottom = new Rectangle(-thicknessWall, -thicknessWall, width, thicknessWall);
  create(pWall, regionWallBottom);

  const regionWallLeft = new Rectangle(-thicknessWall, 0, thicknessWall, regionInner.height);
  create(pWall, regionWallLeft);

  const regionWallRight = new Rectangle(regionInner.right, 0, thicknessWall, regionInner.height);
  create(pWall, regionWallRight);

pWallは、水槽の壁粒子を表す配列です。ここでは、下図のような３領域に分けて粒子を配置しています。

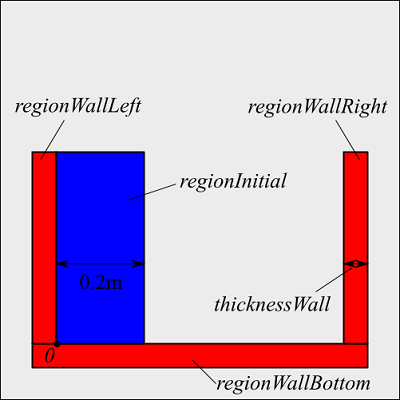
各領域は矩形なので、水槽内側の左下角を原点座標として幾何学的な位置はすぐに計算できると思います。

境界条件

SPH法における壁の取り扱いは、様々な手法が考えられています。今回のように壁も粒子で表すものや、壁から受ける力を与えるものなど様々です。また、壁を粒子でモデル化する場合でも、その計算の仕方によりいろいろな方法が提唱されています。

ここでは、壁での計算を簡易的に行うために、以下のような取り扱いをします。

壁も粒子を配置する。今回は粒子４つ分。
壁粒子も流体粒子と同じ密度、圧力計算を行う。粘性係数も同じ値を持たせる。
固定された壁粒子は静止しており、粒子速度は常にゼロである。

こうすることで、壁で特別な取り扱いをすることなく、流体粒子の計算をすることができます。流体粒子の密度や力を計算するときには、壁粒子も近傍粒子として計算をします。そのために、影響半径$h$以上の厚みを持つように壁粒子を配置しています。

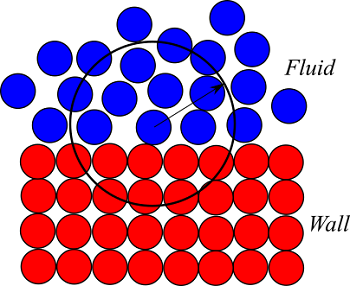
計算上は、壁付近に流体粒子が集中すると、壁粒子の密度、圧力が大きくなります。これにより結果的に壁に侵入しようとする力が妨げられ、流体粒子が壁を通過しないようになります。

まとめ

粒子の初期条件や境界条件について説明しました。これで、プログラムもいよいよ大詰めです。あとは、可視化の部分を作り、全体をつなげると完成です。

←前回　Leap-Frog法で運動方程式を解く
 →次回　粒子の可視化

全体の目次