前回は定常熱伝導方程式を変形し、有限体積法のベースとなる積分形で表しました。
今回は有限体積のメッシュについてお話したいと思います。
目次
メッシュ
前回のシリーズで差分法で離散化したとき、空間を格子状に分割し各点で値を計算していきました。有限体積法はコントロールボリュームの微小要素で空間を分割していきます。その分割した状態のものをメッシュ(Mesh)と呼んでいます。空間を分割してメッシュを作成することをメッシュをきるとよくいいます。
要素の種類
分割されたコントロールボリュームの各要素は様々な形をしています。代表的なものは4面体のテトラ(Tetra)、6面体のヘキサ(Hexa)、多面体のポリへドラル(Poly、 Polyhedron)メッシュなどがあります。
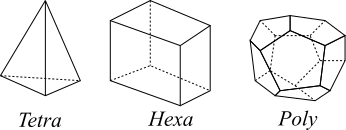
有限体積法は任意の多面体が扱えるようになっているので、自由曲面を持つような複雑な形状に対しても空間を埋めることができます。
構造格子と非構造格子
空間を四角形の要素で埋めていくメッシュを構造格子(Structured Grid)と呼んでいます。構造格子は縦横に四角形の要素(ヘキサメッシュ)が規則正しく並んでいるメッシュです。プログラム上の取り扱いが容易で計算速度も速いですが、複雑な形状の空間を埋めていくことは難しいです。
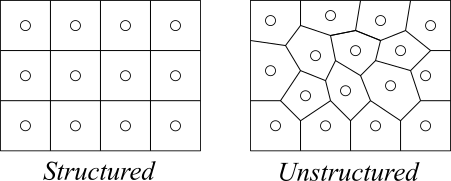
一方、任意の多面体で構成されたメッシュを非構造格子(Unstructured Grid)といいます。任意形状の要素で計算するためプログラム上複雑な処理をする必要がありますが、複雑な形状をもつ空間も柔軟に埋めることができるためよく使われています。
この講座では2次元の矩形の板を計算するため構造格子を使って計算していきます。
メッシュの構成要素
ここでメッシュを構成する要素について抑えておきましょう。構成要素がどのように呼ばれているかを説明します。これらの呼び方は、ソフトウェアや本によって結構バラバラで、ごっちゃになって使われていますが、だいたいどのような呼び方をしているかを知っておくと、様々な場面でとっつきやすくなります。
まずメッシュですが、
メッシュ(Mesh)、グリッド(Grid)、格子
などいろいろ呼ばれています。
次に、コントロールボリュームの各要素ですが、
コントロールボリューム、セル(Cell)、要素(Element)
などと呼ばれます。この講座では主にセル(Cell)と呼ぶことにします。
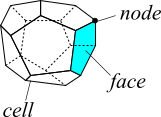
セルを構成している面については、
面、フェース(Face)
と呼んでいます。
セルは頂点を持っています。この頂点は、
ノード(Node)、節点、Vertex
などと呼ばれます。
またメッシュの一番外側の面は境界条件を指定する面になりますが、
境界面、Boundary face
といいます。
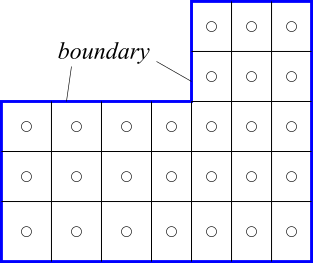
いろいろな呼び方があり一見ややこしいですが、あまり神経質にならずに使ってみてください。
まとめ
有限体積法のメッシュについてお話しました。また各構成要素の呼び方についてもご紹介しました。
次回は有限体積法の離散化に入っていきたいと思います。
