前回は解きたい熱伝導の問題を示し、有限体積法の導入部分をお話しました。
今回は有限体積を具体的な数式で表していきたいと思います。
目次
熱伝導方程式
今回は熱伝導の問題なので、熱伝導方程式を考えましょう。前シリーズで1次元の熱伝導方程式を導出しました。
$$\rho C_p \frac{\partial T}{\partial t} = \lambda \frac{\partial^2 T}{\partial x^2} + q \tag{2-1}$$
$T$は温度、$\rho$は密度、$C_p$は比熱、$\lambda$は熱伝導率、$q$は発熱量を表します。
この式を3次元に拡張した一般的な式は、
$$ \frac{\partial ( \rho C_pT)}{\partial t} = \nabla \cdot (\lambda \nabla T)+ q \tag{2-2}$$
となります。
ベクトル場の発散
ここで、$\nabla$ という記号は、$x$、$y$、$z$それぞれの偏微分を表しています。
$$\nabla T = \left( \frac{\partial T}{\partial x}, \frac{\partial T}{\partial y}, \frac{\partial T}{\partial z} \right) \tag{2-3}$$
$\cdot$ はベクトルの内積を表していて、ベクトル ${\bf a}$ に対して、
$$\nabla \cdot {\bf a} = \frac{\partial a_x}{\partial x} + \frac{\partial a_y}{\partial y} + \frac{\partial a_z}{\partial z} \tag{2-4}$$
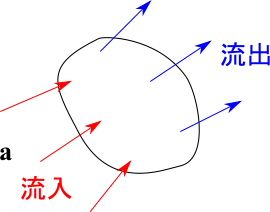
となります。これはベクトル場の発散と呼ばれています。発散といっても、計算が破綻してしまうことではありません。ベクトル場の発散は、ある領域から流入流出する量を表しているとイメージしてください。つまりベクトル ${\bf a}$ に対して、
- $\nabla \cdot {\bf a} > 0$ であれば ${\bf a}$ が湧き出している。出ていく量が多い。
- $\nabla \cdot {\bf a} < 0$ であれば ${\bf a}$ が吸い込まれている。入ってくる量が多い。
- $\nabla \cdot {\bf a} = 0$ であれば流入流出が同じで釣り合っている。
ということを意味しています。
温度の式に戻ると、
となります。温度勾配 $-\lambda \partial T / \partial x$ は移動する熱量を表しているので、結局この項は熱の出入りの関係を意味しています。前シリーズの方程式の導出を再度復習してみてください。
(ちなみに、この項は温度の2階微分なので、差分法ではこの項を中心差分で離散化し計算しましたね。)
定常熱伝導方程式
今回は定常状態の温度を求めます。定常状態とは時間変化のない状態のことです。つまり(2-2)式の左辺はゼロになります。そして、熱の発散項を左辺に持ってくると、(2-2)式は次のように書けます。
$$-\nabla \cdot (\lambda \nabla T) = q \tag{2-6}$$
これが定常の熱伝導方程式です。
積分形式
ここで微小な領域を考えましょう。この微小領域の体積を $V$、面を $S$ で表します。この領域に対して(2-6)式を考えます。
体積積分
微小領域内で(2-6)式の各量がいくらになるかを計算してみます。
例えば右辺の発熱量 $q$ は、式上は単位体積あたりの発熱量です。[W/m3] といった単位になります。領域内での総発熱量 $Q$ を求めるためには、体積積分をして求めます。
$$Q = \int_{V} q dV \tag{2-7}$$
積分は高校で習うはずなので、ぜひ思い出してください。この体積積分は、$q$ に微小な体積 $dV$ を掛けて、領域内全体で総和をとるというイメージです。$\int_{V}$ は領域内での体積積分を表します。
左辺も同様に体積積分すると次の式になります。
$$- \int_{V} \nabla \cdot (\lambda \nabla T) dV = \int_{V} q dV \tag{2-8}$$
発散定理(ガウスの定理)
(2-8)式の左辺は発散の体積積分になっています。ここで発散定理(ガウスの定理(Gauss' theorem) とも言う)を使います。発散定理は発散の体積積分を面積積分で表すものです。
$$\int_{V} \nabla \cdot {\bf a} dV = \int_{S} {\bf a} \cdot d {\bf S} \tag{2-9}$$
前述のように発散とは、ある量(ここでは ${\bf a}$)の出入りを表すものでした。つまり発散の体積積分は、領域全体で ${\bf a}$ が増減した量を表しています。一方で、保存則から領域全体での ${\bf a}$ の増減量は、領域の面をとおして ${\bf a}$ が出入りした量の総和に等しいです。面をとおして出入りした量の総和というのは、まさに面積積分のことです。
要するに発散定理は、
(領域全体で ${\bf a}$ が増減した量)=(領域の面をとおして ${\bf a}$ が出入りした量)
を表していることになります。

(ちなみに $d {\bf S}$ は微小面積ですが、$S$ の面に垂直なベクトルとして定義されます。つまり、${\bf a} \cdot d {\bf S}$ は、${\bf a}$ の面に垂直な成分と微小面積 $dS$ の積を表しています。)
では、この発散定理を用いて(2-8)式を書き直してみると、次のようになります。
$$- \int_{S} (\lambda \nabla T) \cdot d{\bf S} = \int_{V} q dV \tag{2-10}$$
もともとの微分方程式(2-6)式は、積分を用いた(2-10)式のように書き表すことができました。このような式を積分形式といいます。
まとめ
今回は数式がたくさん出てきました。定常熱伝導方程式を変形し積分形式で書き表しました。有限体積法ではこの形式をベースとして離散化していきます。次回は有限体積法の離散化の前段階としてメッシュについてお話したいと思います。
