目次
はじめに
科学技術計算講座も4回目のシリーズに突入です。これまで、オイラー法やルンゲ=クッタ法による常微分方程式の数値計算、差分法による熱伝導計算など様々な数値計算法を学んできました。
第4回目のシリーズは「有限体積法で熱伝導シミュレーション」です。前回に続き身近な熱伝導現象を有限体積法という手法を使って計算してみます。今回もPythonを使って実際にプログラムを作りながら計算手法を学んでいきましょう。
問題
早速、今回解きたい問題を提示します。
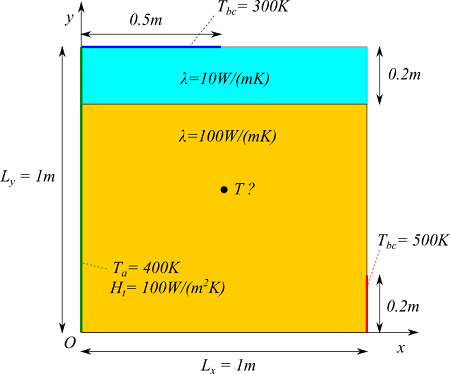
前シリーズで計算した2次元熱伝導の問題に似ていますが、境界条件が増えています。また、熱伝導率が違う複数の部材の組み合わせになっています。さらに、定常状態(時間変化しない)での温度を求めるという部分が異なります。
前回作った差分法のプログラムを改良していけば解くことはできますが、今回は「有限体積法」という別の解法で解いてみることにしましょう。
このシリーズでは、2次元定常熱伝導の問題を有限体積法を使ってPythonで解く、というのを目的としたいと思います。そのために必要な数式や解法、プログラムなどをその都度説明していきます。簡単な題材で有限体積法とはどのようなものかを理解していきましょう。
有限体積法とは
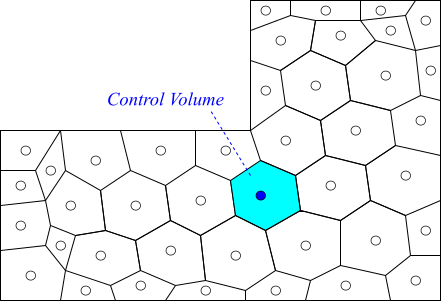
有限体積法(Finite Volume Method、FVM)は、解析領域を有限個のコントロールボリューム(Control Volume、CV)に分割し、それぞれのCVで保存則を考え離散化していく手法です。計算する物理量はコントロールボリュームの中心で値を持ちます(中心以外で値を持たせる方法もあります)。CVは任意の多面体を考えることができるので、複雑形状の解析対象に対しても柔軟に対応できます。
流体解析の世界では、OpenFOAMや商用の流体解析ソフトのほとんどで有限体積法が採用されています。当サイトのオンライン熱流体解析ツールCATCFDzeroも有限体積法で解いています。
一方、構造解析(材料力学)の世界では、よく似た言葉で有限要素法(Finite Element Method、FEM)という手法が使われます。これも解析領域を微小要素に分割しますが、有限要素法は分割された各要素の中の物理量を補間関数で近似して解いていきます。ここでは詳しく説明しませんが、有限要素法と有限体積法は全く別の解析手法です。
コントロールボリュームでの保存則
有限体積法の基本的なコンセプトは、コントロールボリューム(CV)内での保存を考えることです。時間変化のない熱の流れを考えましょう。発熱がない場合、CVに流入してくる熱量と流出する熱量はイコールで釣り合っています。つまり、流出する熱量から流入する熱量を引いたものはゼロになります。
(流出する熱量)-(流入する熱量)=0
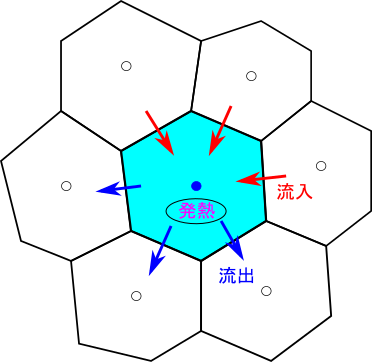
CV内で発熱があると、流出する熱量はその分だけ多くなるので、
(流出する熱量)-(流入する熱量)=(発熱量)
となります。これは熱の保存則を意味します。
有限体積法ではこのような保存則に基づいた定式化をしていきます。したがって、コントロールボリューム内で物理量の保存が保たれています。
まとめ
有限体積法についての導入部分をお話しました。有限体積法はコントロールボリュームでの保存を考えたコンセプトになっています。
次回は有限体積法の定式化について説明したいと思います。
