前回は完全陰解法による熱伝導方程式のプログラミングを行い、大きな時間刻みでも安定に計算できることを確認しました。
今回はクランク=ニコルソン法という解法をご紹介します。
目次
ちょっとその前に用語の話
これまでいろいろな数値計算法を学んできました。オイラー法とかルンゲ=クッタ法とかFTCS法や陰解法などなど。数値計算法は数値解法と言ったりします。また、これらの解法はスキームと呼ばれています。
スキームは差分法のことを呼ぶときにも使います。差分スキームと呼んだりもします。前進差分や中心差分も差分スキームの一種です。
またヤコビ法やガウス=ザイデル法のような連立方程式(線形代数方程式と言います)を解く解法をアルゴリズムと呼んだりもします。
数値計算の世界ではこれらの用語を結構ごちゃまぜで使っていることが多いので、あまり神経質にならずにいろいろな呼び方があるなくらいに思っていてください。
スキームの精度について
以前、オイラー法よりルンゲ=クッタ法の方が計算精度が高いというお話をしました。数値計算のスキームは時間方向にも空間方向にも離散化して差分で表しているため、必ず誤差が生じます。どのくらいの誤差が生じるかというのは、テイラー展開という数学の処理を行って調べることができます(またもやここではやりません)。
それによると差分スキームの精度は次のようになっています。
前進差分: $(y_{i+1}-y_i)/\Delta x$ →1次精度
後退差分: $(y_{i}-y_{i-1})/\Delta x$ →1次精度
中心差分: $(y_{i+1}-y_{i-1})/(2\Delta x)$ →2次精度
次数が高くなるにしたがって計算精度が高くなります。ちなみに、4次のルンゲ=クッタ法は4次精度です。
次数とは誤差が $\Delta x$ の何乗に比例するかというオーダーのことです。1次精度は $\Delta x$ の1乗、2次精度は $\Delta x$ の2乗に比例した誤差を含んでいます。$\Delta x$ を小さくしていくと次数の高い方が急速に誤差は小さくなっていくので、次数が高いと計算精度が高くなります。
オイラー法は時間に対して前進差分をとっているので1次精度です(※)。4次のルンゲ=クッタ法に比べて計算精度が悪いというわけです。
FTCS法は時間に対しては1次精度の前進差分、空間に対しては2次精度の中心差分をとっています。時間的な精度が低いので、このスキームは1次精度です。完全陰解法も時間に対して1次の後退差分を使っているので、FTCS法と同じく1次精度です。
では陰解法でもう少し精度の高い方法はないでしょうか。ここでは2次精度のクランク=ニコルソン法をご紹介します。
※ 前進差分や後退差分も2次や3次といった高次の差分で表現することも可能です。ここでは上記の形式の1次精度のものを前進差分、後退差分と呼んでいます。
数値計算が使われる分野によりどこまでの精度を求めるかはさまざまですが、CAE分野の流体解析など一般に使われる範囲では、高くてもせいぜい2次精度というのが多いです。
クランク=ニコルソン法
クランク=ニコルソン法(Crank-Nicolson Method)は時刻 $n+1/2$ に対して、時間は2次の中心差分、空間も2次の中心差分をとったスキームです。
ただし、時刻 $n+1/2$ という点は存在しない点なので、空間差分を時刻 $n$ と $n+1$ の平均をとった形をしています。
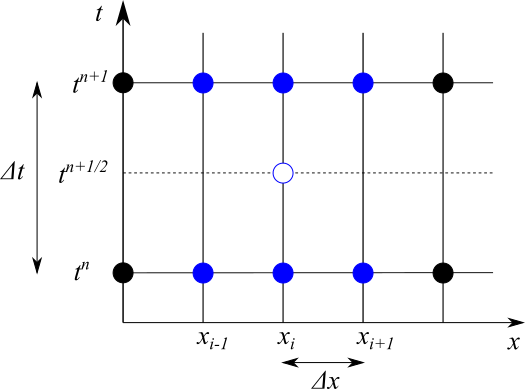
(1)式を書き換えると、
となり、さらに反復法で扱いやすいように変形すると、
と表せます。ここで、$c = \alpha \Delta t/ \Delta x^2$。クランク=ニコルソン法は、時間も空間もどちらも2次なので2次精度です。完全陰解法にくらべ精度が高いので比較的よく使われるスキームです。
クランク=ニコルソン法は陽解法と陰解法を合わせたような形をしています。このスキームも安定性解析で安定性を調べると、無条件安定であることがわかっています。つまり時間刻みを大きくとっても安定に計算できます。
プログラミング
クランク=ニコルソン法をプログラミングしてみましょう。完全陰解法のプログラムを少し変更するだけです。
temp[i] = 1.0 / (1.0 + ck) * ((1.0 - ck) * temp_old[i] \
+ 0.5 * ck * temp_old[i+1] + 0.5 * ck * temp_old[i-1] \
+ 0.5 * ck * temp[i+1] + 0.5 * ck * temp[i-1])ガウス=ザイデル法のループの中を(3)式に書き換えてください。今回は式が長いので途中で改行しています。 途中で改行する場合は、\ (バックスラッシュ)を行の最後に入れて改行して続けます。
計算結果
プログラムをPythonで計算してみてください。結果は次のようになりました。
まとめ
今回はクランク=ニコルソン法を紹介し、計算精度について説明しました。これで空間分布を持つ問題について、陽解法、陰解法といったスキームを一通り学んだことになります。これだけできれば、いろいろな問題をプログラミングして数値計算することができると思います。
さてせっかくなので、最後に今回の問題を2次元に拡張してみたいと思います。1次元だと線のグラフでしたが、2次元にしてカラーのアニメーション表示もしてみましょう。次回は熱伝導方程式の2次元への拡張についてお話します。
