前回は惑星の運動方程式を導き、無次元化により計算しやすいシンプルな方程式にしました。
本日は、いよいよPythonで地球の軌道計算をするプログラムを作成します。
目次
惑星の運動方程式のおさらい
今回解く運動方程式をおさらいしておきます。
無次元化した惑星の運動方程式は、
$$\frac{d \vec{v_*}}{dt_*}=- \frac{\vec{r_*}}{r_*^3} \tag{1}$$
$$\frac{d \vec{r_*}}{dt_*}=\vec{v_*} \tag{2}$$
でした。* は無次元化された量を意味し、次の規格化定数を掛けると実際の物理量になります。
$$ r_0 = 1.496 \times 10^{11}\rm[m]$$
$$v_0 = 2.979 \times 10^4 \rm[m/s]$$
$$t_0 = 5.022 \times 10^6 \rm[s] = 58.13 \rm[day]$$
$r_0$は太陽と地球の距離、$v_0$は地球の公転速度、$2\pi t_0$が地球の公転周期になります。
ベクトルを計算する
これを今までと同じようにプログラミングしていけばよいのですが、この式にはベクトルが含まれています。まず、Pythonでベクトルをどのように扱うかを説明しておきます。
ベクトルとは、大きさと方向を持っていて、成分で表すことができる量です。2次元平面の位置ベクトルは、
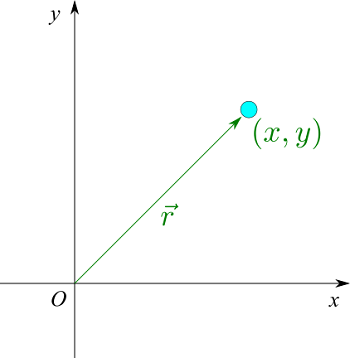
$$\vec{r} = (x, y) \tag{3}$$
のように、x、y 座標で表すことができます。これは、原点から点 $(x, y)$ に向かう矢印で表せます。
ベクトルは普通の数と同じように、ベクトルどうし足したり引いたりすることができます。また、ある値を掛けたり割ったりすることもできます。
ベクトルの足し算をしてみましょう。次のような2つのベクトル
$$\vec{a} = (1, 2) \tag{4}$$
$$\vec{b}=(3,4) \tag{5}$$
を足すと、
$$\vec{a} + \vec{b} = (1+3, 2+4) = (4, 6) \tag{6}$$
と計算できます。ベクトルの各成分どうしを足せばよいのです。引き算も同じです。各成分どうしを引き算します。
次に、ベクトルにある値を掛けてみます。例えば 5 を $\vec{a}$ に掛けると、
$$ 5 \ \vec{a} = (5 \times 1, 5 \times 2) = (5, 10) \tag{7}$$
となります。ベクトルの各成分に値をかければよいのです。割り算も各成分を割れば求められます。 ちなみに、ここで掛けた 5 という量は、ベクトルではなくスカラーと呼ばれます。スカラーは方向を持たない、いわゆる普通の値です。
(ここで注意ですが、ベクトル同士の掛け算というのは、ちょっと難しいです。単純に成分同士を掛けるというのではありません。内積とか外積と呼ばれる計算をするのですが、今回は必要ないのでここでは触れません。また、ベクトル同士の割り算というのは、そもそも出来ません。)
Pythonでベクトルの計算を行うには、numpyというライブラリを使用します。(6)式の計算をするプログラムは次のように書けます。
import numpy as np
a = np.array([1, 2])
b = np.array([3, 4])
c = a + b
print(c)まず、import numpy as np で numpyをインポートします。
$\vec{a}$ は、a = np.array([1, 2]) というように定義します。$\vec{b}$ も同じように b = np.array([3, 4]) で定義します。足し算は普通に足せばよく、c = a + b と書きます。すると、c には a と b の各成分が足されたベクトルが入ります。printの出力結果は、[4 6] となっています。
(7)式を計算するプログラムは次のようになります。
import numpy as np
a = np.array([1, 2])
c = 5 * a
print(c)この出力結果は、[ 5 10] となっていますね。この場合も c はベクトルです。
このように Python では簡単にベクトルの計算ができます。各成分ごとに演算しなくてよいのでプログラムを簡潔に書くことができます。ただし、プログラム中の変数がベクトルなのか、スカラーなのか注意しておいてください。
惑星の運動方程式をプログラミング
では、惑星の運動方程式、(1)(2)式をルンゲ=クッタ法を使って書いてみましょう。(ファイル出力やグラフ出力は省いています。)
import numpy as np
# parameter
r = np.array([0.0, 1.0])
v = np.array([-1.0, 0.0])
t = 0.0
dt = 0.001
nt = 10000
# function
def fr(v):
return v
def fv(r):
rnorm = np.linalg.norm(r)
return -r / rnorm**3
# time loop
for i in range(nt):
rp = r
vp = v
kr1 = fr(vp)
kv1 = fv(rp)
rp = r + 0.5 * dt * kr1
vp = v + 0.5 * dt * kv1
kr2 = fr(vp)
kv2 = fv(rp)
rp = r + 0.5 * dt * kr2
vp = v + 0.5 * dt * kv2
kr3 = fr(vp)
kv3 = fv(rp)
rp = r + dt * kr3
vp = v + dt * kv3
kr4 = fr(vp)
kv4 = fv(rp)
r += dt * (kr1 + 2.0 * kr2 + 2.0 * kr3 + kr4) / 6.0
v += dt * (kv1 + 2.0 * kv2 + 2.0 * kv3 + kv4) / 6.0
t += dt全体の流れは、2回目で作った減衰振動プログラムとほとんど同じです。
import numpy as npまず、numpyをインポートします。
r = np.array([0.0, 1.0])
v = np.array([-1.0, 0.0])位置 r、速度 v はベクトルとして定義します。ここでは初期値として、$\vec{r} = (0.0, 1.0)$、$\vec{v} = (-1.0, 0.0)$ を与えています。
その後の、t とか dt はベクトルではありません。
nt = 10000nt はforループの繰り返し回数です。今までは、for文に直接書いていましたが、変更しやすいように変数にしてみました。
def fr(v):
return v
def fv(r):
rnorm = np.linalg.norm(r)
return -r / rnorm**3 ここは関数の定義です。fr は(2)式の右辺を、fv は(1)式の右辺を表しています。引数の v や r はベクトルです。return で返す量もベクトルになります。
fv内の rnorm = np.linalg.norm(r) は、$\vec{r}$ の大きさ(絶対値、ノルムともいう)を計算しています。np.linalg.norm() はベクトルの大きさを計算する関数です。
(ちなみに、fr は v をそのまま返すだけなので関数にする必要はないのですが、fvと合わせるためにあえて関数にしています。)
rp = r
vp = v
kr1 = fr(vp)
kv1 = fv(rp)ルンゲ=クッタ法の第1ステップの計算です。r、v はベクトルなので、代入した rp、vp もベクトルになります(*)。また、fr、fv関数はベクトルを返すので、kr1、kv1 もベクトルになります。
rp = r + 0.5 * dt * kr1
vp = v + 0.5 * dt * kv1
kr2 = fr(vp)
kv2 = fv(rp)ルンゲ=クッタ法の第2ステップ以降も同様に計算していきます。
* Pythonではベクトルのような配列をそのまま別の変数に代入する場合と、何か計算してから代入する場合では、厳密には違いがあります。参照渡しと呼ばれますが、rp = r のようにそのまま代入した場合、rp は r そのものを表しています。つまり、rp の要素を一部変更してしまうと、元の r の値も変わってしまいます。ここでは詳細は省きますが、rp の要素の一部を変更するような操作が入る場合は注意が必要です。このプログラムでは関係ありません。
r += dt * (kr1 + 2.0 * kr2 + 2.0 * kr3 + kr4) / 6.0
v += dt * (kv1 + 2.0 * kv2 + 2.0 * kv3 + kv4) / 6.0
t += dt最後に各値を更新しています。ここでは、累算代入演算子+= を使っています。t += dt は t = t + dt のように、左辺の変数に右辺を足した後、同じ変数に入れるというものです。
まとめ
Pythonでベクトルを扱う方法を説明して、ルンゲ=クッタ法で運動方程式をプログラミングしました。基本的な部分はできたので、次回はこれを計算してみましょう。せっかくなので、地球の運動の様子をアニメーションで表示してみたいと思います。
