【科学技術計算講座1-9】応用問題１～熱伝達による温度変化

ここまでで、微分方程式をオイラー法を使ってPythonでシミュレーションできるようになりました。一分子反応のような形の微分方程式は、１階常微分方程式と呼ばれています。このようなタイプであれば２つの変数を同時に解く連立方程式も、オイラー法を使って解くことができることも学びました。

今回は他の物理現象を同じような形をした微分方程式で表し、シミュレーションしてみたいと思います。

鉄球はどれくらいで冷える？

ここでは、温度の問題を取り上げてみましょう。

問題：100℃に熱した直径１cmの鉄球を、20℃の流体中に置いた時、温度変化を求めたい。ただし、熱伝達率を400 [W/(m² K)] とする。

温度の高い鉄球が流体中に置かれたとき、周囲の温度が低ければ、熱は鉄球から流体中に伝わり鉄球の温度の温度は下がっていきます。

数式を導出する

まず、これを解くための数式を考えなければなりません。

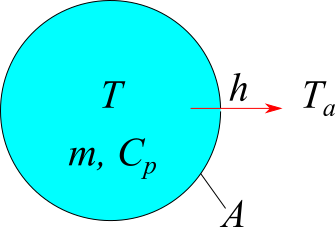
温度変化というのは、すなわち熱エネルギーの変化に相当します。鉄球の質量を $m$ [kg]、比熱を $C_p$ [J/(kg K)]、温度を $T$ [K]とすると、鉄球の持つ熱エネルギーは、$m C_p T$ [J] です。熱エネルギーの時間変化は、これまでやってきたように時間の微分で表せるので、

$$m C_p \frac{dT}{dt} \tag{1}$$

となります。$m$ と $C_p$ は時間変化しないとして、微分の外に出しています。この量の単位は [J/s]、つまり [W] です。

次に右辺を考えましょう。鉄球の熱は周りの流体中に逃げていくのですが、逃げていく熱量は鉄球の温度と流体の温度との差に比例していると仮定します。つまり、温度差が大きいと熱逃げが大きいだろうというわけです。また、鉄球の表面積が大きいほど、熱逃げは大きくなるでしょう。とすると、熱の変化は、①鉄球と周囲流体の温度差と②鉄球の表面積に比例すると考えられます。これを数式で表すと、

$$ h A (T_a - T) \tag{2}$$

となります。ここで、$T_a$ は周囲流体の温度[K]、$T$ は鉄球の温度[K]、$A$は鉄球の表面積 [m²]、$h$は比例係数です。

(1)式と(2)式をイコールでつなぐと、

$$m C_p \frac{dT}{dt} = h A (T_a - T) \tag{3}$$

という微分方程式になります。左辺の単位が [W] だったので、$h$ の単位は [W/(m² K)] であることがわかります。そうこの $h$ が、熱伝達率と呼ばれているものです。

ここで、(3)式の両辺を $m C_p $ で割って、ちょっとだけ変形してみます。

$$\frac{dT}{dt} = \frac{h A}{m C_p} (T_a - T) \tag{4}$$

少し形が違いますが、一分子反応の方程式によく似た形が出来上がりました。これが今回計算する微分方程式です。

条件を整理する

この式を計算するために条件を整理してみます。

初期条件は、鉄球の温度 $T$ = 100 [℃] です。

周囲温度 $T_a$ = 20 [℃]、熱伝達率 $h$ = 400 [W/(m² K)] です。

鉄球の直径が１cm なので、表面積 $A$ [m²] は求められますね。

質量 $m$ [kg] は、鉄なので密度を 7870 [kg/m³] として計算してください。比熱 $C_p$ は、442 [J/(kg K)] としましょう。

何秒間の計算をするかは、温度変化の結果をみながら調整してみてください。

これだけあれば、計算することができます。これまでに作ったプログラムを参考に、この問題を解くプログラムを作ってみてください。

プログラム

プログラムの参考例を載せておきます。

import matplotlib.pyplot as plt
import csv
import math

# parameter
temp = 100.0
ta = 20.0

h = 400.0

time = 0.0
dt = 0.1

d = 0.01
den = 7870.0
cp = 442.0
area = math.pi * d**2
vol = math.pi * d**3 / 6.0 
mass = den * vol

# graph data array
gtime = []
gtemp = []

# csv file
outfile = open('output.csv','w', newline='')
writer = csv.writer(outfile)
writer.writerow(['i', 'time', 'temperature'])

# time loop
for i in range(1000):
    ft = h * area * (ta - temp) / (cp * mass)
    temp = temp + dt * ft
    time = time + dt

    print('i: {0:4d}, time: {1:6.2f}, temp: {2:9.6f}'.format(i, time, temp))

    gtime.append(time)
    gtemp.append(temp)

    writer.writerow([i, time, temp])

outfile.close()

# graph plot
plt.plot(gtime, gtemp)
plt.xlabel('Time')
plt.ylabel('Temperature')
plt.legend(['T'])
plt.show()

→プログラムはこちら（GitHub）

プログラムの骨格は、これまでに作ったものとほとんど同じです。

違うところは、まず時間の変数を t から time に変えました。温度が $T$ という記号なので、紛らわしいので time にしました。

そして、温度は temp という変数にしました。今回は方程式が一つなので、解く変数は temp だけです。

あと表面積と質量をプログラムの以下の箇所で計算しています。

d = 0.01
den = 7870.0
cp = 442.0
area = math.pi * d**2
vol = math.pi * d**3 / 6.0 
mass = den * vol

表面積は、area ですが、直径 d から計算させています。このとき、円周率 $\pi$ が必要ですが、Pythonでは円周率を math.pi で取得できます。math.pi を使うには、プログラムのはじめに import math と書いておきます。あとは同様に体積 vol を計算して、質量 mass を求めています。表面積も質量も手計算して与えてやってもよいのですが、せっかくなのでプログラム内で計算するように作ってみるとよいでしょう。

計算結果

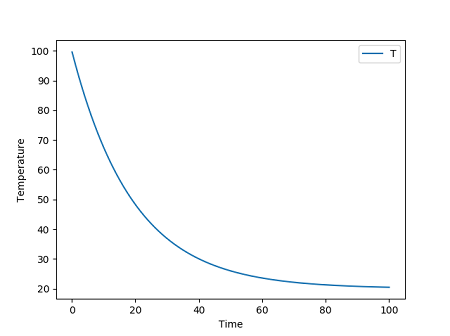
計算して出力されたグラフです。初期に100℃だった温度は徐々に低下していき、100秒ほどで周囲温度と同じ20℃になっていることがわかりました。

仮定について

ここで、ちょっと注意です。今回計算に使った(4)式の方程式ですが、これには幾つもの仮定が入っています。

鉄球の温度は一様である
鉄球は３次元の球体なので、中心部分と表面では温度が違います。表面付近の方が早く冷えていくはずです。しかし、ここでは鉄球の温度はどこでも一様としていて、一つの温度しか持っていません。
周囲流体の温度は変わらない
20℃の流体（空気とか水とか）中に100℃の物体を置くと、流体は温められ物体の周りの流体温度は上昇するはずです。水だと沸騰することもあるでしょう。ここでは、そこまで考えないで流体温度は一定で変わらないとしているのです。
物性値や熱伝達率は変わらない
比熱などの物性値は温度によって変化します。また、熱伝達率も温度や流体の流れ方により変化します。ここでは、そういった変化は考えず一定としています。

他にも球の熱膨張とか実際の現象では起こっていることを考えていません。物理現象から方程式を立てるときは、このように様々な仮定が入っているのです。すべて現実に忠実にやろうとすると、ありとあらゆる物理現象を考えなければならず、計算式は膨大になっていきます。そこで、あまり影響のなさそうなものは考えず、数式をシンプルにしています。これをモデル化と言ったりします。

計算結果も、これらの仮定を考慮した上での結果であることを忘れないでください。もし、実現象でこれらの仮定の影響が大きい場合、実際の鉄球の温度変化から計算結果はずれてくるでしょう。

まとめ

今回は応用問題として熱伝達による鉄球の温度変化を計算してみました。物理現象と方程式の立て方、仮定についても説明しました。基本的な問題でしたが、数値計算の基礎となるものがたくさん詰まっています。

次回は、【科学技術計算講座１】の最終回です。もうひとつ応用問題を解いてみたい思います。

←前回　計算結果の精度

→次回　応用問題２～ばねの運動方程式

全体の目次