前回は解きたい問題を数式で表しました。
今回は、作った数式をどのように計算するかを説明します。
目次
数値計算法
前回、考えた一分子反応の数式は、
$$\left\{ \begin{aligned} \frac{d [\rm{A}]}{dt} &= -k [\rm{A}]\\ \frac{d [\rm{B}]}{dt} &= k [\rm{A}] \end{aligned} \right. \tag{1}$$
という微分方程式でした。
数学の問題であれば、この式を積分して解くことになります。実際、この微分方程式は簡単に積分することができます。なので、実はわざわざコンピュータで解く必要はないのです。でも、それではこの講座は終わってしまいますので、これをコンピュータでどのように計算していくかを説明していきます。
ある方程式が与えられた時に、コンピュータなどで数値的に解く方法を数値計算法といいます。(1)式のような微分方程式を解くための数値計算法はたくさん考えられています。今回は、最初なので最も簡単なオイラー法という方法を使って解くことにしましょう。
オイラー法
オイラー法は、(1)式のような微分方程式を解くための計算法です。一般的に、次のような微分方程式を考えます。
$$\frac{dy}{dt} = f(t, y) \tag{2}$$
(1)式と比べると、$y$ は濃度 $[\rm{A}]$、$f(t, y)$ は関数を表していて $-k [\rm{A}]$ に対応しています。
(1)式は濃度の時間あたりの変化量を表しているんでしたね。同じように(2)式は $y$ の時間あたりの変化量を表しています。ある時刻 $t$ の変化量がわかっているので、これで1秒後の $y$ の値は計算できます。
今、ある時刻を $t_n$ 、そのときの $y$ の値を $y_n$ とします。すると、時間あたりの変化量は、$f(t_n, y_n)$ となります。では、$h$ 秒後の $y$ を計算しましょう。時間あたりの変化量が $f(t_n, y_n)$ なので、時間 $h$ を掛けると正味の変化量になります。$y_n$ にこの変化量を加えてやれば $h$ 秒後の $y$ が求まります。
$$y_{n+1} = y_n + h f(t_n, y_n) \tag{3}$$
$$t_{n+1} = t_n + h \tag{4}$$
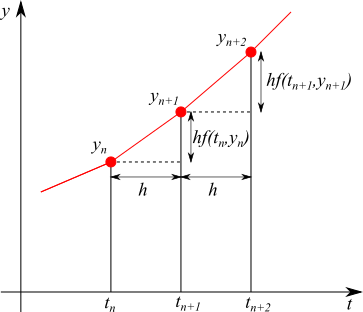
ここで、$h$ 秒後の $y$ を $y_{n+1}$ 、時刻を $t_{n+1}$ としています。図で表すとこんな感じです。

これを見ると、$f(t_n, y_n)$ は、時刻 $t_n$ のときの、$y$ の傾きを表していることがわかります。$y_{n+1}$ がわかれば、さらに $h$ 秒後の $y_{n+2}$ も同じように求まります。時間は $h$ の間隔で進んでいき、そのときの $y$ の値が、時々刻々求まるというわけです。
(3)式を計算するのは簡単です。最初の時刻 $t_0$ (普通は0秒です)のときの $y$ を $y_0$ とすると、$h$ 秒後は、
$$y_1 = y_0 + h f(t_0, y_0) $$
その次の $h$ 秒後は、
$$y_2 = y_1 + h f(t_1, y_1) $$
それ以降、
$$y_3 = y_2 + h f(t_2, y_2) $$
$$y_4 = y_3 + h f(t_3, y_3) $$
$$...$$
と、次々に $y$ の値を求めることができます。このように、微分方程式がわかっていれば、最初の初期値を与えてやるだけで、芋づる式に計算することができるのです。これがオイラー法です。
この方法を使えば、特に積分なんてしなくても、値を求めることができてしまいます。また、このような繰り返し計算は、電卓をたたいて手で計算してもいいのですが、コンピュータに自動で計算させれば楽ちんです。つまり、このオイラー法をプログラミングしてコンピュータに計算させてしまおうというのが、数値計算なのです。
時間変化を計算していくタイプの数値計算法は他にもたくさんありますが、その多くはオイラー法のように時々刻々ステップ式に計算していく手法です。時間は $h$ 秒ごとに計算されるので、その間の時間は計算されません。このようにステップごとに計算することを離散化といいます。$h$ を大きくとれば間隔が粗くなりますが、$h$ を小さくすれば間隔が小さく滑らかになることは、すぐにイメージできると思います。$h$ のとり方による違いはまた今度お話したいと思います。
問題の数式をオイラー法で書いてみる
では、(1)式を(3)(4)式のオイラー法の形に書き直してみましょう。
ここで、ちょっと注意なのですが、(1)式はAとBの2つの濃度に対する微分方程式になっています。これは連立方程式なので、AとBの2つを同時に解く必要があります。と言っても、難しくはありません。オイラー法に沿って計算するだけです。
(2)式の $f(t,y)$ の関数は、(1)式の右辺に相当するので、AとBに対してそれぞれ関数を用意して、
$$f_{A,n} = -k [{\rm{A}}]_n \tag{5}$$
$$f_{B,n}= k [{\rm{A}}]_n \tag{6}$$
とします。
あとは、(3)(4)式と同じように書くと、
$$[{\rm{A}}]_{n+1} = [{\rm{A}}]_n + \Delta t \ f_{A,n} \tag{7}$$
$$[{\rm{B}}]_{n+1} = [{\rm{B}}]_n + \Delta t f_{B,n} \tag{8}$$
$$t_{n+1} = t_n + \Delta t \tag{9}$$
となります。ここで、(3)式の $h$ は時間の間隔でしたが、これを $\Delta t$ に書き換えています。数値計算では、この $\Delta t$ のことを時間刻みと呼んでいます。(5)~(9)式が、今回解く方程式のオイラー法の形になります。
まとめ
今回は微分方程式を解く方法として、オイラー法を説明しました。ここまでで、プログラミングに入る前段階は終了です。いよいよ次回から、Pythonを使って「一分子反応の微分方程式をオイラー法で解く」というのをプログラミングする作業に入りたいと思います。
