科学技術計算講座の第1回目のシリーズも本日で最後になりました。今までで、オイラー法を使って、微分方程式をPythonでプログラミングして、計算できるようになりました。
今回は、応用問題の2問目としてばねの運動方程式を解いてみたいと思います。
目次
ばねの運動
ばねは力学の問題の中でも基礎的なもので、高校の物理でも出てくると思います。では、今日の問題です。
方程式を導出する
さていつものように、方程式を導出してみましょう。物体の運動を表す式は、運動方程式といいます。高校の物理で習いましたね。運動方程式はご存知の通り、
$$ma=F \tag{1}$$
です。$m$ は質量、$a$ は加速度、$F$ は力です。質量 $m$ の物体に、力 $F$ を加えると、加速度 $a$ が生じるということを表しています。
ところで、この講座で学んできた微分方程式は、求めたい変数を時間で微分した形になっていました。この運動方程式も微分方程式の形で表したいです。ここで、加速度というのは、速度の時間変化を意味しています。ということは、(1)式は速度を $v$ とすると、
$$m \frac{dv}{dt} = F \tag{2}$$
と書くことができます。次に右辺の力 $F$ について考えましょう。球には、ばねによる力(復元力)が働きます。これも高校で習いましたが、ばねの復元力は、
$$-kx$$
です。ここで、$k$ はばね定数、$x$ はばねの伸び(変位といいます)を表しています。伸びれば伸びるほど力が大きくなるので、伸びに比例しています。(縮む場合も同じ。)符号がマイナスなのは、ばねの伸び(変位)に対して反対向きに力がかかることを意味しています。
簡単なばねの問題なら力はこれだけなのですが、今回はもう一つ摩擦力がかかると言っています。摩擦力は速度に比例するとあるので、
$$-cv$$
と書きましょう。$c$ は比例係数です。これも符号がマイナスになっていますが、これは速度の向きに対して、反対方向にかかる力だからです。
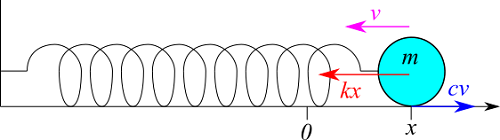
この2つの力が加わるので、(2)式は次のようになります。
$$m \frac{dv}{dt} = -kx-cv \tag{3}$$
これが、球に対する運動方程式になります。今までと同じような微分方程式の形をしていますね。これで、オイラー法で解けそうですが、ちょっと待ってください。ばねの変位 $x$ はどうすればよいでしょうか。(3)式は速度に対する微分方程式になっていますが、これだけでは $x$ が求まりません。
$x$ に対しては次のように考えます。そもそも速度 $v$ というのはどういう量かというと、変位 $x$ の時間変化のことです。時間変化は微分のことだったので、
$$\frac{dx}{dt} = v \tag{4}$$
という式が成り立ちます。(3)式と(4)式を連立して解いてやると、変位 $x$ も速度 $v$ も同時に求まります。連立方程式はこれまでやってきたので計算できますね。このようにして、運動方程式は $x$、$v$ の連立方程式として数値計算できます。
条件を整理する
条件を整理しておきます。初期条件は、変位 $x$ = 0.1 です。速度は、手を離しただけなので、$v$ = 0.0 です。球の質量は $m$ = 1.0、ばね定数 $k$ = 0.2、摩擦力の比例係数 $c$ = 0.1 です。計算する時間は結果をみて調整しましょう。
$x$ と $v$ をグラフにして、球がどのような動きをするのかみてみましょう。
今回もプログラムを作って計算してみてください。
プログラム
プログラムの参考例を載せておきます。
import matplotlib.pyplot as plt
import csv
# parameter
x = 0.1
v = 0.0
t = 0.0
k = 0.2
c = 0.1
m = 1.0
dt = 0.1
# graph data array
gt = []
gx = []
gv = []
# csv file
outfile = open('output.csv','w', newline='')
writer = csv.writer(outfile)
writer.writerow(['i', 't', 'x', 'v'])
# time loop
for i in range(1000):
fx = v
fv = (-k * x - c * v) / m
x = x + dt * fx
v = v + dt * fv
t = t + dt
print('i: {0:4d}, t: {1:6.2f}, x: {2:9.6f}, v: {3:9.6f}'.format(i, t, x, v))
gt.append(t)
gx.append(x)
gv.append(v)
writer.writerow([i, t, x, v])
outfile.close()
# graph plot
plt.subplot(2,1,1)
plt.plot(gt, gx)
plt.ylabel('x')
plt.legend(['x'])
plt.grid()
plt.subplot(2,1,2)
plt.plot(gt, gv)
plt.xlabel('Time')
plt.ylabel('v')
plt.legend(['v'])
plt.grid()
plt.show()プログラムは、これまでとほぼ同じです。ただ、グラフのところだけちょっと変えています。$x$ と $v$ は違う物理量で大きさも異なるので、一つのグラフにすると見にくいです。そこで、別々のグラフとして同時に出力しています。ここでは、
plt.subplot(2,1,1)
plt.subplot(2,1,2)
のように subplot を使っています。subplot(n, m, i) は、「グラフを n行×m列 に分割した i 番目のウィンドウに出力する」、という意味です。今回の場合は、2行×1列の1番めに $x$ を2番めに $v$ を出力しています。
grid() はグリッド線を表示しています。
計算結果
計算結果は次のグラフのようになりました。
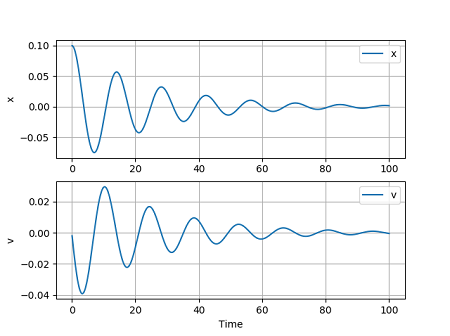
変位 $x$ は、0.1 から徐々に減少していき、-0.075くらいになり(マイナスはばねが縮んでいる状態)、再び増加します。しかし、もとの 0.1 になることはなく、0.057くらいまでしか増加しません。そのあとも、振動していきますが、変位の最大は徐々に小さくなっていきます。これは、球に摩擦力が働いているためです。摩擦による抵抗力が働かないと、球は振動を続けますが、抵抗力があると振動は減衰していきます。これを減衰振動といいます。
速度 $v$ は、初速 0 からマイナスの方向(縮む方向)に増加し、同様に減衰しながら振動しています。
最後は原点の位置で球は止まってしまいます。
数値計算の精度
以前、数値計算精度についてお話しました。この計算結果についてはどうでしょうか。実は減衰振動も厳密解があります。今回の条件では、
$$ x = a e^{-\gamma t} \cos(\sqrt{\omega^2-\gamma^2} t + \alpha)$$
となります。ここで、$a = \sqrt{\omega^2 x_0^2/(\omega^2-\gamma^2)}$、$\alpha = \tan^{-1} (-\gamma / \sqrt{\omega^2-\gamma^2})$、$x_0 = 0.1$、$\gamma = c/(2m)$、$\omega = \sqrt{k/m}$。
厳密解と計算結果を比較してみると次の図のようになります。
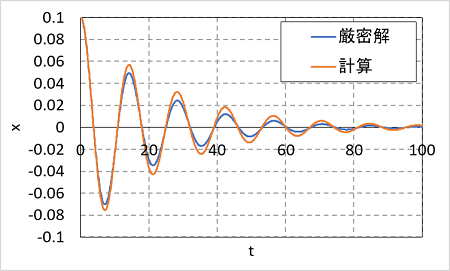
振動の振幅が少し計算の方が大きいです。これは、以前お話したオイラー法の計算精度の問題点です。変化が大きいと、このように誤差が大きくなってしまいます。振動のだいたいの様子は捉えられていますが、細かい数値を議論したいときは、もっと精度のよい数値計算法を使った方がよさそうです。他の数値計算法については、またいずれお話したいと思います。
数値計算の手順
これまでの講座で、数値計算やシミュレーションについて、基礎となる部分を説明してきました。
まとめると、数値計算の流れは、
- まず、問題に対してどのような物理現象になるかを考える
- 次に、物理現象を表す方程式はどのようなものかを考える
- そして、立てた方程式を数値的に解くための解法を考える
- それから、プログラミングして計算する
- 最後に、計算結果を評価する
となるのです。要するに数値計算とはプログラミングだけやってもだめなのです。最初に言いましたが、1,2はとても重要で、3までできると仕事が終わったも同然です。あとは、プログラミングして計算するのみです。最後の評価は、1,2の物理や数式、そのときの仮定がわかっていないとできませんし、3の計算精度や誤差がわかってないと結果の正しさがわかりません。もちろんこの後、計算結果をどのように活かすかは皆さんの腕の見せどころです。
このように、プログラミングだけでなく、物理や数学、数値計算法など様々なところに気を配りながらシミュレーションしていただければと思います。
この第1回目の講座では、ある程度簡単な方程式や数値解法で説明してきましたが、数値計算の流れを掴む基礎となるものだったと思います。これだけで、結構いろいろな計算ができるはずです。
また第2回目もこのような数値計算について学んでいきたいと思います。
