
目次
エージェントベースモデルによる牧羊犬のシミュレーション
広い牧場で多くの羊を放牧する場合、羊の群れを目的地に誘導するのに、牧羊犬が使われている。犬は巧みに行動し、多くの羊がいる群れをうまく誘導していく。
ここでは、牧羊犬が羊を目的地まで誘導していく様子を数値計算でシミュレーションしてみる。
モデルはエージェントベースモデルを使う。エージェントベースモデルとは、個々の個体の運動をモデル化し、複数の個体を同時に計算することで、全体の様子をシミュレーションするものである。牧羊犬のシミュレーションは文献[1][2]を参考に次のようなモデルとした。
羊のモデル
羊は次のルールに従って行動する。
(S1)近くの羊と近づきすぎない
(S2)群れようとする
(S3)犬が来ると逃げる
これを表現するために以下のような数学モデルを考える。
平面内に $N$ 頭の羊が存在する。$i$ 番目の羊は、位置ベクトル $P_i$ と速度ベクトル $V_i$ を持つ。時間は離散的に逐次計算とする。まず、個々の羊がそれぞれのルールに従いどの方向に移動するかを計算する。各ルールによる移動方向をそれぞれ $\hat{v}_1$、$\hat{v}_2$、$\hat{v}_3$ とすると、速度はその線形の重ね合わせで表すこととする。
$w_0, w_1, w_2, w_3$ は重み係数、$n$ は時間ステップ、^ は単位ベクトルを意味する。各ルールの移動方向は次のように計算する。
(S1)近くの羊と近づきすぎない
羊は自分の周りの羊と適度な距離を保とうとする。羊は自分の位置 $P_i$ から距離 $d_{ss}$ 内にいる他の羊の位置 $P_j$ から離れる方向に移動する。羊が複数いる場合は、距離の2乗で割って重み付けし、重ね合わせたベクトル方向に移動する。これを数式で表すと以下のようになる。
$$ v_1 = -\sum_j \frac{P_j - P_i}{|P_j - P_i|^2} \tag{2}$$
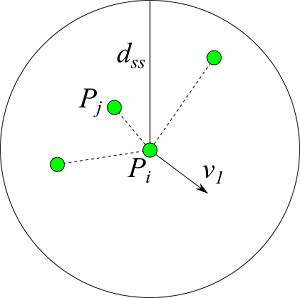
また、羊は近くに犬がいる場合(距離 $d_{dg}$ 以内に犬がいる場合)は、$d_{ss}$ を小さくとり隣の羊と密集する。
(S2)群れようとする
羊は群れで行動しようとする。羊は距離 $d_{gr}$ 内にいる他の羊が作る群れの重心位置 $P_G$ に向かって移動する。
$$ v_2 = P_G - P_i \tag{3}$$
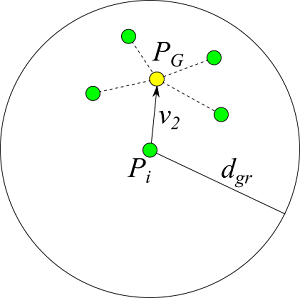
なお、近くに犬がいない場合は群れる効果は大きくないが、近くに犬がいる場合は集団で行動しようとするため、$w_2$ を大きくしてより集まろうとする。
(S3)犬が来ると逃げる
近くに犬がいると犬と反対方向に逃げようとする。
$$ v_3 = -(P_{dg} - P_i) \tag{4}$$
$P_{dg}$ は犬の位置ベクトル。
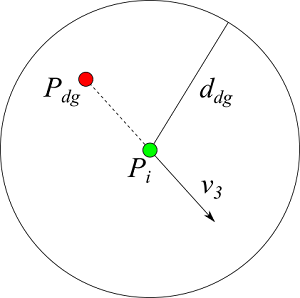
次のステップの速度は(1)式で計算する。各移動方向は単位ベクトルに規格化した後、重み係数($w_1, w_2, w_3$)をかけて足し合わせる。このとき、前ステップの移動方向を $w_0$ の重みをつけて足し合わせる。羊の速度は、大きくなりすぎないように最大速度 $V_{max}$ に制限される。$V_{max}$ は、犬が近くにいるときは大きく、犬がいないときは小さい値とする。
羊の次のステップの位置は次式で計算される。
$$P_i^{n+1} = P_i^n + V_i^n \Delta t \tag{5}$$
$\Delta t$ は時間刻みである。
犬のモデル
犬は羊をまとめて目的地に誘導することが役目である。そこで、犬は3つのルールに従って行動することとした。
(D1)羊と近づきすぎない
(D2)群れ全体を目的地に誘導する
(D2')群れから外れた羊を群れに戻す
羊と同様に、犬の速度 $U$ は次式で計算する。
$$U ^{n+1}= z_0 \hat{U}^n + z_1 \hat{u}_1+z_2 \hat{u}_2 \tag{6}$$
$z$ は重み係数、$u$ は各ルールの移動方向。
(D1)羊と近づきすぎない
犬は羊に近づきすぎないようにする。犬は最も近い羊が距離 $d_{sd}$ 内にいるときは、その羊と反対方向に移動しようとする。
$$ u_1 = -(P_i - P_{dg}) \tag{7}$$
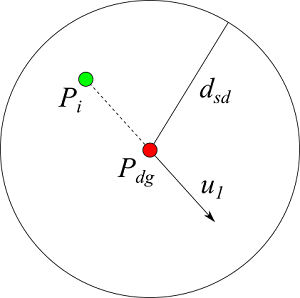
(D2)群れ全体を目的地に誘導する
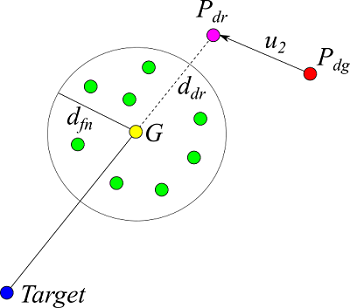
まず、犬は自分から最も近い羊の周り $d_{gr}$ 内の距離にいる羊を群れと認識する。次に、その群れが重心から 距離 $d_{fn}$ 内に収まっていれば、群れがまとまっていると認識する。そして、目標地点から重心 $G$ を結ぶ直線の後方 $d_{dr}$ 離れた地点 $P_{dr}$ に移動して、群れを目標に向かわせようとする。
このときの犬の移動方向は次のようになる。
$$ u_2 = P_{dr} - P_{dg} \tag{8}$$
(D2’)群れから外れた羊を群れに戻す
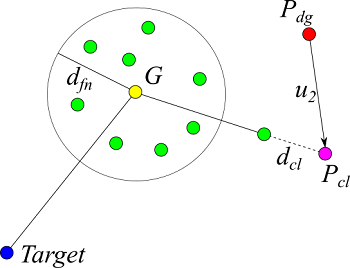
もし、羊の群れが $d_{fn}$ 内に収まっていなければ、(D2)の行動をとらずこちらの行動をとるものとする。ここでは、群れから最も外れている羊に近づき群れにもどす働きをする。群れの重心から一番遠い羊に引いた直線の後方 $d_{cl}$ 離れた地点 $P_{cl}$ に移動して、その羊を群れに戻そうとする。移動方向は次式となる。
$$ u_2 = P_{cl} - P_{dg} \tag{9}$$
犬の速度も最大速度 $U_{max}$ を持ち(6)式で計算される。同じく犬の位置も次式で逐次計算される。
$$P_{dg}^{n+1} = P_{dg}^n + U_i^n \Delta t \tag{10}$$
境界条件
空間は $L \times L$ の2次元平面とする。領域の境界は壁があるものとし、羊、犬とも境界に到達すると垂直方向の速度を反転させる。完全反射と同じイメージ。
初期条件
羊はある領域にランダムに配置し初速をゼロとした。犬も初速ゼロで、羊の群れから離れた場所にいるものとした。
パラメータ
今回の計算に用いたパラメータを表に示す。
| パラメータ | 内容 | 値 |
|---|---|---|
| $L$ | 空間サイズ | 200 m |
| $\Delta t$ | 時間刻み | 1 s |
| $N$ | 羊の数 | 50 |
| $d_{ss}$ | 羊どうしの距離 | 5 m (犬がいないとき) 2 m (犬がいるとき) |
| $d_{gr}$ | 羊の群れのサイズ | 30 m |
| $d_{dg}$ | 羊が犬を認識する距離 | 50 m |
| $w_0$ | 重み係数(前ステップ速度V) | 0.5 |
| $w_1$ | 重み係数(S1) | 2 |
| $w_2$ | 重み係数(S2) | 0.01(犬がいないとき) 1.05(犬がいるとき) |
| $w_3$ | 重み係数(S3) | 0(犬がいないとき) 1(犬がいるとき) |
| $V_{max}$ | 羊の最大速度 | 0.5 m/s(犬がいないとき) 3 m/s(犬がいるとき) |
| $d_{sd}$ | 犬が保とうとする羊との距離 | 2 m |
| $d_{dr}$ | 犬が群れの後方に位置する距離 | 10 m |
| $d_{cl}$ | 犬が外れた羊の後方に位置する距離 | 5 m |
| $d_{fn}$ | 犬がまとめようとする群れのサイズ | 15 m |
| $z_0$ | 重み係数(前ステップ速度U) | 1.5 |
| $z_1$ | 重み係数(D1) | 1.5 |
| $z_2$ | 重み係数(D2) | 3 |
| $U_{max}$ | 犬の最大速度 | 6 m/s |
結果
結果を動画で示す。緑が羊、赤が犬を表している。左下角が目標地点だ。
最初、犬は散らばっている羊を一つの小さな群れにまとめる。そのあと、群れの後方に位置しながら、目標地点に群れを誘導していく。途中、群れから離れる羊がでるが犬はその羊に近づき、うまく群れに戻しながら、群れ全体を目標地点に誘導している。なかなか優秀な牧羊犬だ。
次に、目標地点が領域の中央にある場合の結果を示す。
最初に群れをまとめて目標まで連れて行くところは同じだが、羊はじっとしていないので最後うまくまとめられず、ちょっと右往左往している。例えば、目標地点に近づくと犬は動きを止めたり、最後は群れの外周を大きく回りながら群れをとどめておくような行動をしたらよいのだろう。まだ新米の牧羊犬なので仕方ない(というか、そのようにプログラムしていないので。。。)。
3D表示
シミュレーション結果を3Dで表示したものも示しておこう。
上の動画はドローンのように俯瞰的に捉えているが、以下のリンクを開くと実際にマウスで回転や移動ができる。いろいろな角度から見ることができるので面白い。
まとめ
このシミュレーション手法を使うことで、比較的単純なルールに従い全体として一つの組織的な行動をシミュレーションできる。パラメータを変えてみたり、行動のルールを変えたりすることで、全体の中で個々の最適な行動パターンを把握することもできる。
参考文献
[1] Strömbom, D.; Mann, R. P.; Wilson, A. M.; Hailes, S.; Morton, J.; Sumpter, D. J.; King, A. J. Solving the shepherding problem: heuristics for herding autonomous, interacting agents. Journal of the Royal Society. Interface. 2014, vol. 11, 20140719. https://doi.org/10.1098/rsif.2014.0719
[2] 東俊一; 田淵絢子; 杉江俊治. 牧羊犬制御のモデル化. 計測自動制御学会論文集. 2012, vol. 48, no. 12, p. 882-888.
