目次
非ニュートン流体の粘度
非ニュートン流体は、せん断速度により粘度が変化し、流体に力を加えると流れ方が変わる性質を持っています。身の回りには、多くの非ニュートン流体が存在します。
非ニュートン流体を表す数値モデルは種々ありますが、ここではよく使われるHerschel–Bulkleyモデルで説明します。
Herschel–Bulkleyモデル
Herschel–Bulkleyモデルは以下の式で表されます。
$$\tau = \tau_0 + K \dot{\gamma}^n$$
$\tau$:せん断応力、$\tau_0$:降伏応力、$K$:コンシステンシーインデックス、$\dot{\gamma}$:せん断速度、$n$:べき乗指数
非ニュートン流体は、せん断速度とせん断応力の関係が非線形となります。
粘度$\mu$で表すと以下の式となります。
$$\mu = \frac{\tau_0}{\dot{\gamma}} + K \dot{\gamma}^{n-1}$$
参考文献: Herschel, W.H.; Bulkley, R. Konsistenzmessungen von Gummi-Benzollösungen. Kolloid Zeitschrift. 1926, vol. 39, p. 291–300.
ニュートン流体 (Newtonian fluid)
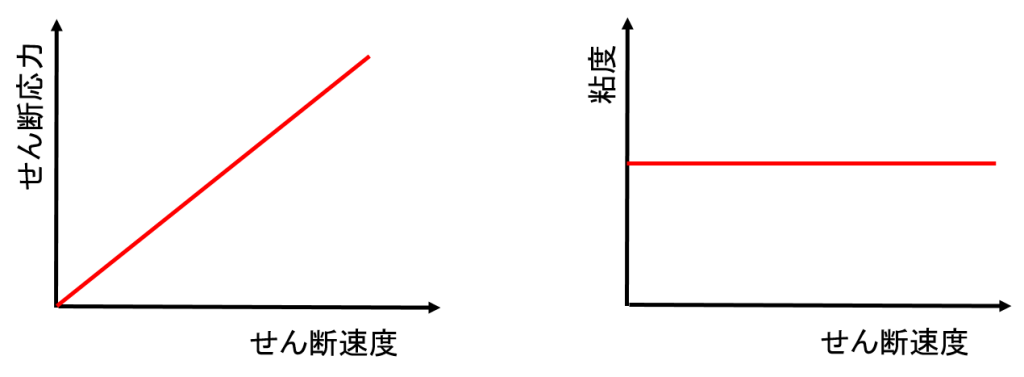
上式で、$\tau_0=0$、$n=1$の時、ニュートン流体を表します。ニュートン流体は、せん断応力はせん断速度と線形の関係にあり、せん断速度によらず粘度は一定となります。
空気や水はニュートン流体として扱われます。
ダイラタント流体 (Dilatant fluid)
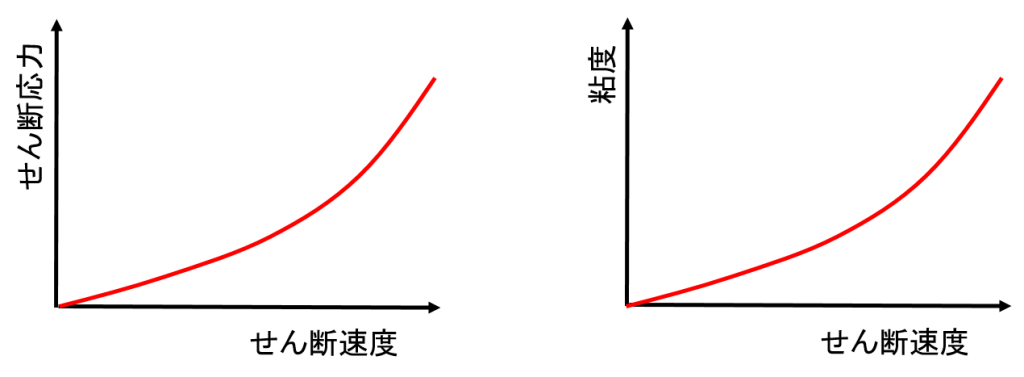
$\tau_0=0$、$n>1$の時、ダイラタント流体と呼ばれます。せん断速度が大きいとせん断応力が急に増加し、粘度も大きくなります。
片栗粉と水を混ぜ合わせたものや、水を含んだ砂など、急に力を加えると固くなり、ゆっくり力を加えるとさらさらと流れる性質をもつものがダイラタント流体です。
擬塑性流体 (Pseudoplastic fluid)
$\tau_0=0$、$n<1$の値を持つものは、擬塑性流体と呼ばれます。せん断速度が大きくなるにつれせん断応力の増加が緩やかになります。力を加えないと粘度が大きく、力を加えると粘度が小さくなるような流体です。
マヨネーズやある種の塗料など、そのままでは粘度が高く流動しにくいですが、力を加えると流れやすくなる性質を持ちます。

ビンガム流体(Bingham fluid)
$\tau_0>0$、$n=1$の時、ビンガム流体と言います。加えた力が小さいと固体として振る舞い、ある力を超えると流動物として振る舞う性質を持っています。せん断応力は、せん断速度ゼロで降伏応力を持ち塑性流体とも呼ばれます。
バターやチューブ入りハミガキなどがビンガム流体と言われています。

せん断応力と粘度のグラフ表示
ここでは、せん断速度に対するせん断応力と粘度をグラフ表示することができます。降伏応力$\tau_0$、指数$n$、コンシステンシーインデックス$K$を入力するとせん断応力$\tau$と粘度$\mu$がグラフ表示されます。グラフのX軸、Y軸の最大値は変更できます。
