目次
断面二次モーメントと断面係数
断面二次モーメントと断面係数、断面積を計算します。形状を選択し、各寸法を入力してください。断面二次モーメントと断面係数、断面積が計算されます。
断面二次モーメントは曲げモーメントに対する梁の変形のしにくさを表します。
断面形状
形状を選択してください。
矩形

断面二次モーメント
$$I = \frac{b h^3}{12}$$
断面係数
$$Z = \frac{b h^2}{6}$$
断面積
$$A=bh$$
| $b$ [mm] | |
| $h$ [mm] | |
| $I$ [mm4] | |
| $Z$ [mm3] | |
| $A$ [mm2] |
矩形(中空)
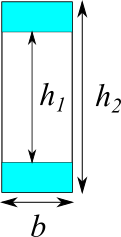
断面二次モーメント
$$I = \frac{b ( h_2^3 - h_1^3)}{12}$$
断面係数
$$Z = \frac{b ( h_2^3 - h_1^3)}{6 h_2}$$
断面積
$$A=b(h_2-h_1)$$
| $b$ [mm] | |
| $h_1$ [mm] | |
| $h_2$ [mm] | |
| $I$ [mm4] | |
| $Z$ [mm3] | |
| $A$ [mm2] |
円
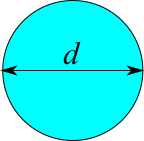
断面二次モーメント
$$I = \frac{\pi d^4}{64}$$
断面係数
$$Z = \frac{\pi d^3}{32}$$
断面積
$$A=\pi \frac{d^2}{4}$$
| $d$ [mm] | |
| $I$ [mm4] | |
| $Z$ [mm3] | |
| $A$ [mm2] |
円(中空)
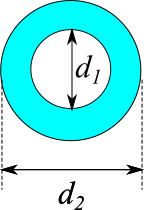
断面二次モーメント
$$I = \frac{\pi (d_2^4 - d_1^4)}{64}$$
断面係数
$$Z = \frac{\pi (d_2^4 - d_1^4)}{32 d_2}$$
断面積
$$A=\pi \frac{d_2^2-d_1^2}{4}$$
| $d_1$ [mm] | |
| $d_2$ [mm] | |
| $I$ [mm4] | |
| $Z$ [mm3] | |
| $A$ [mm2] |
楕円
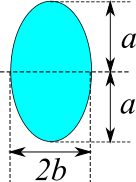
断面二次モーメント
$$I = \frac{\pi a^3 b}{4}$$
断面係数
$$Z = \frac{\pi a^2 b}{4}$$
断面積
$$A=a b \pi$$
| $a$ [mm] | |
| $b$ [mm] | |
| $I$ [mm4] | |
| $Z$ [mm3] | |
| $A$ [mm2] |
三角形
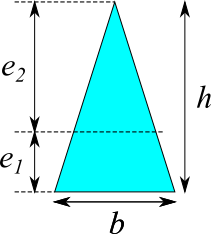
断面二次モーメント
$$I = \frac{b h^3}{36}$$
断面係数
$$Z_1 = \frac{b h^2}{12},\quad Z_2 = \frac{b h^2}{24}$$
$$e_1 = \frac{h}{3},\quad e_2 = \frac{2 h}{3}$$
断面積
$$A=\frac{1}{2}bh$$
| $h$ [mm] | |
| $b$ [mm] | |
| $e_1$ [mm] | |
| $e_2$ [mm] | |
| $I$ [mm4] | |
| $Z_1$ [mm3] | |
| $Z_2$ [mm3] | |
| $A$ [mm2] |
台形
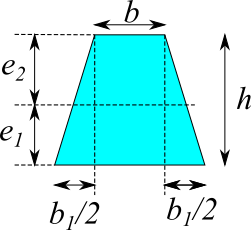
断面二次モーメント
$$I = \frac{6 b^2 + 6 b b_1 + b_1^2}{36 (2 b + b_1)} h^3$$
断面係数
$$Z_1 = \frac{I}{e_1},\quad Z_2 = \frac{6 b^2 + 6 b b_1 + b_1^2}{12 (3 b + 2 b_1)} h^2$$
$$e_1 = h - e_2,\quad e_2 = \frac{3 b + 2 b_1}{3 (2 b + b_1)} h$$
断面積
$$A=\frac{1}{2}(2b+b_1)h$$
| $h$ [mm] | |
| $b$ [mm] | |
| $b_1$ [mm] | |
| $e_1$ [mm] | |
| $e_2$ [mm] | |
| $I$ [mm4] | |
| $Z_1$ [mm3] | |
| $Z_2$ [mm3] | |
| $A$ [mm2] |
H形、十字形
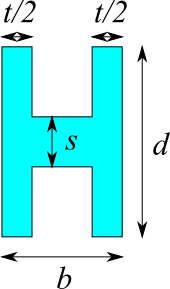

断面二次モーメント
$$I = \frac{t d^3 + s^3 (b-t)}{12}$$
断面係数
$$Z =\frac{t d^3 + s^3 (b-t)}{6 d}$$
断面積
$$A=td+s(b-t)$$
| $t$ [mm] | |
| $b$ [mm] | |
| $s$ [mm] | |
| $d$ [mm] | |
| $I$ [mm4] | |
| $Z$ [mm3] | |
| $A$ [mm2] |
I型
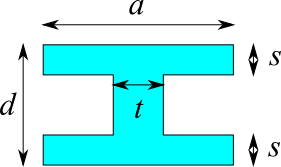
断面二次モーメント
$$I = \frac{a d^3-h^3(a-t)}{12}$$
ここで、$h=d-2s$
断面係数
$$Z =\frac{a d^3-h^3(a-t)}{6 d}$$
断面積
$$A=2as+ht$$
| $t$ [mm] | |
| $a$ [mm] | |
| $s$ [mm] | |
| $d$ [mm] | |
| $I$ [mm4] | |
| $Z$ [mm3] | |
| $A$ [mm2] |





