パイプラインやノードの連結構造などで、上流のノードから順番に計算したい場合があります。上流の計算結果を下流のノードに受け渡したい場合などです。
このような構造でノードの計算順序を上流から並べるアルゴリズムを考えます。
データ構造
次のようなデータ構造を考えます。

A~Iまでの9個のノードが連結しています。矢印は連結の方向を表します。例えば、AはCから流入し、Fへ流出しています。FはAから流入し、IとDへ分岐して流出しています。ピンク色のCとEは連結の最初の流入ノードを表しています。また、青色のHとGは一番下流の終端ノードを表します。
さて、このようなデータ構造で上流から順番に順序を付けるにはどのようにすればよいでしょうか?
まず、各ノードがどのノードへ流出するか(もしくは、どのノードから流入するか)という連結情報がわかっているとします。流入ノードがなければ最上流のノードになり、流出先がなければ終端のノードであることは、すぐに判定できます。
CとEは最初のノードなので、仮にCからたどって行くとします。まずC、A、Fとたどります。次にFはDとIに分岐しています。もし、Dを先にたどると失敗します。なぜなら、DはBからも流入しますが、Bの上流にはIがあるからです。つまり、IとBを先にたどった後で、Dをたどる必要があります。
このモデルでは、ノードの数も少なく分岐も少ないため、簡単そうに見えますが、ノードや分岐が多い場合や分岐先が別の枝に接続するような複雑なモデルでは、順序を決める法則を見つけるのが難しいです。
アルゴリズム
ここでは、このように連結されたノードの計算順序を上流から順番に並べる方法を説明します。
ここで説明するのは、ノードの接続を一つずつ見ていき、順番を並べ替える手法ではなく、反復計算を用いて、順序を算出するアルゴリズムです。
1. 順序を表す量を0に初期化
まず、ノードに順序を表す量を持たせます。最初に全てのノードで、この量(順序量と呼ぶことにします)を0に初期化しておきます。
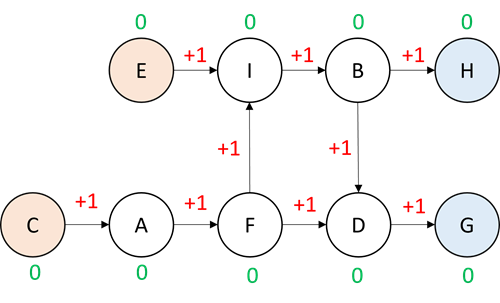
緑:順序量
2. 上流から順序量を受け取る
ノードは上流のノードから順序量を受け取ります。このとき、上流ノードの順序量に1を足した量を受け取ります。複数のノードから流入がある場合は、それらの量を合計します。受け取った量をそのノードの新たな順序量とします。
これを、全ノードについて計算します。ノードの計算の順番は何でもよいですが、このモデルではアルファベット順(A、B、・・・、H、I)としておきます。
最初のステップで全ノードについて計算すると、次の図のように順序量が決まります。
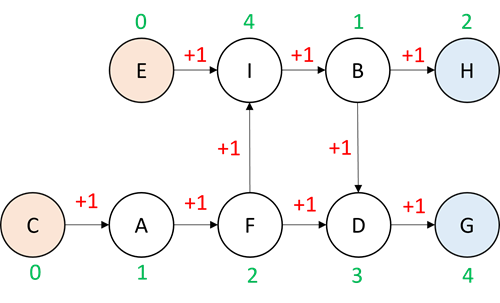
※順序量を計算する際、上流側のノードがすでに更新されていれば、その順序量を使っています。
3. 順序量が変化しなくなるまで繰り返す
この計算を順序量が変化しなくなるまで繰り返します。
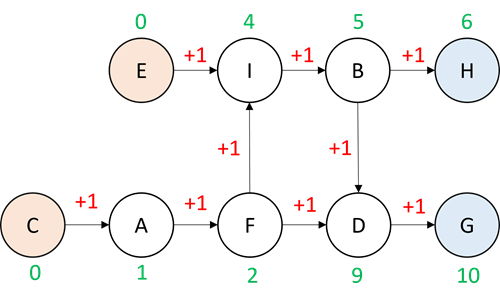
4. 順序量が小さい順に並べる
収束したらノードを順序量が小さい順に並べます。このモデルでは以下の順序になります(括弧内は順序量)。
C(0)、E(0)、A(1)、F(2)、I(4)、B(5)、H(6)、D(9)、G(10)
※順序量が同じ場合は、別途何かのルールで決めます。
これで、上流から順番に並べることができます。この順序でノードをたどると、あるノードを処理する際には、全ての上流ノードの処理が必ず終わっている状態となります。
注意事項
ただし、このアルゴリズムでは注意点があります。上記の反復計算が収束するためには、必ず上流から下流へ向かって道筋が一意に連結している必要があります。
次の図を見てください。

FはAとIから流入し、Dへ流出しています。DはBへ流出し、BはIにつながっています。そして、Iは再びFに流入します。つまり、Fの上流をたどると、F自身につながっています。
モデルに、このような再循環(フィードバックループ)があると、上記の反復計算は収束しません。そもそも上流から下流への順序が一意に決まらないためです。
今回のアルゴリズムで反復計算が収束しなかった場合は、このような再循環を含むことが考えられます。
