今回は行列のQR分解について解説します。
目次
QR分解とは
行列は二つの行列の積に分解するという操作がよく出てきます。線形方程式の解を求めるときに役立つものとしてLU分解というのがあります。LU分解は与えられた行列を下三角行列と上三角行列の積に分解するものです。詳細は以下の記事を参照ください。
ここではQR分解について解説します。QR分解とは行列${\bf A}$を直行行列${\bf Q}$と上三角行列${\bf R}$の積に分解するものです。
$${\bf A}={\bf Q}{\bf R} \tag{1}$$
QR分解は行列の固有値を求めるQR法や最小二乗法を解く際に使われます。
QR分解の方法はいくつかありますが、ここではハウスホルダー変換(Housefolder transformation)を用いた方法をご紹介します。これ以外にもグラムシュミット直交化(Gram–Schmidt orthonormalization)による方法もあります。
ハウスホルダー変換とは
ハウスホルダー変換とは、あるベクトル${\bf x}$を鏡映変換でベクトル${\bf y}$にする変換です。
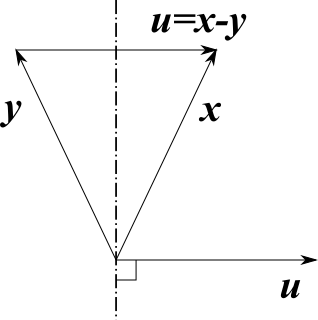
このときの変換行列を${\bf H}$とすると、
$${\bf y} = {\bf H}{\bf x} \tag{2}$$
と書けます。${\bf y}$から${\bf x}$に向かうベクトルを${\bf u} = {\bf x}- {\bf y}$とすると、変換行列は
$$ {\bf H} = {\bf I} - \frac{2 {\bf u} {\bf u}^{\rm T}}{|| {\bf u}||^2} \tag{3}$$
となります(${\bf I}$は単位行列)。この行列${\bf H}$をハウスホルダー行列といいます。
ハウスホルダー行列は対称行列
$${\bf H} ={\bf H}^{\rm T} \tag{4}$$
でかつ、直行行列
$${\bf H}^{-1} ={\bf H}^{\rm T} \tag{5}$$
という性質を持っています。
ハウスホルダー変換によるQR分解
このハウスホルダー変換を用いてQR分解を行う方法を見ていきます。
いま、$N \times N$の正方行列${\bf A}$を
としたとき、この行列を上三角行列${\bf R}$に変換することを考えます。
上三角行列は下半分の三角部分の要素が全てゼロになっている行列です。
まずはじめに、行列${\bf A}$の一列目をベクトル${\bf a}_1 = (a_{11}, a_{21}, \cdots , a_{N1})^{\rm T}$とみなし、ハウスホルダー変換${\bf H}$によって、次式のように最初の要素以外がゼロとなるベクトルに変換できたとします。
$${\bf H} {\bf a}_1 = \left(\begin{array}{c} ||{\bf a}_1|| \\ 0\\ \vdots \\ 0 \end{array}\right) \tag{8}$$
ここで、変換後のベクトルの最初の要素は元のベクトル${\bf a}_1$の大きさになっています(変換前後でベクトルの大きさを一致させるため)。
ハウスホルダー行列${\bf H}$は、(3)式から${\bf x}={\bf a}_1$、 ${\bf y} = (||{\bf a}_1||, 0, \cdots , 0)^{\rm T}$として求めることができます。
ここで、最初の行列を${\bf A}^{(0)}$、上記のハウスホルダー行列を${\bf H}^{(1)}$と書くことにします。上の添字はステップの回数を表します。
ハウスホルダー行列${\bf H}^{(1)}$を行列${\bf A}^{(0)}$に作用させると、
となり、1列目は一番上の要素以外はゼロになっています。他の要素は、最初の行列要素からは変わっているため、上添字を付けています。
次に2列目の2行目より下をゼロにしていきます。これは同様に${\bf x}={\bf a}_2^{(1)} = (a_{22}^{(1)}, a_{23}^{(1)},\cdots , a_{N2}^{(1)})^{\rm T}$から${\bf y} = (||{\bf a}_2^{(1)}||, 0, \cdots , 0)^{\rm T}$への変換を考えます。
ここでは、$a_{22}^{(1)}$要素から右下部分の要素が変換できればよいことに注意してください。この変換行列を${\bf H'}^{(2)}$とすると、
$${\bf H}^{(2)}=\left(\begin{array}{cc}1 & 0 \\ 0 & {\bf H'}^{(2)} \end{array}\right) \tag{10}$$
と書け、これを(9)式に作用させると、
となります。あとは同様に順次これを繰り返していきます。k回目のステップの変換行列は、
$${\bf H}^{(k)}=\left(\begin{array}{cc}{\bf I}& 0 \\ 0 & {\bf H'}^{(k)} \end{array}\right) \tag{12}$$
と表され、これを$N-1$回作用させると、上三角行列
が求まります。
次に行列${\bf Q}$ですが、(13)式の右辺の${\bf H}$の逆行列を左辺の${\bf R}$に作用させると、
となり、(1)式の定義から、
と求まります。なお、(15)式はハウスホルダー行列が直行行列かつ対称行列であるという性質から、$ {\bf Q} ={\bf H}^{(1)} {\bf H}^{(2)} \cdots {\bf H}^{(N-1)}$と同じです。
QR分解は要素の符号を除いて一意に決まります。また、ここでは正方行列を考えましたが、一般に$M \times N$ $(M \ge N)$の行列に拡張できます。
QR分解のPythonプログラム
ハウスホルダー変換によるQR分解をPythonでプログラミングしてみます。早速ですが、プログラムを以下に示します。
import numpy as np
# sign function
def sign(x):
if x >= 0:
return 1
else:
return -1
# input matrix
a = np.array([[1., 5., 4.],
[2., 4., -7.],
[2., 7., 14.]])
n = a.shape[0]
# QR decomposition by Householder transformation
r = a.copy()
q = np.eye(n)
u = np.zeros(n)
for k in range(n-1):
# |x|
absx = 0
for i in range(k, n):
absx += r[i][k]**2
absx = np.sqrt(absx)
if absx == 0:
continue
# u=x-y
u[k] = r[k][k] + sign(r[k][k]) * absx
absu = u[k]**2
for i in range(k+1, n):
u[i] = r[i][k]
absu += u[i]**2
# H=I-2uu'/|u|^2
h = np.eye(n)
for i in range(k, n):
for j in range(k, n):
h[i][j] -= 2 * u[i] * u[j] / absu
r = np.dot(h, r)
q = np.dot(q, h)
print("Q =\n", q, "\n")
print("R =\n", r, "\n")
print("QR =\n", np.dot(q, r), "\n")以下説明していきます。
# input matrix
a = np.array([[1., 5., 4.],
[2., 4., -7.],
[2., 7., 14.]])
n = a.shape[0]最初の行列をa、行列の大きさをnとします。
r = a.copy()
q = np.eye(n)
u = np.zeros(n)rは最終的に上三角行列になります。最初はaを入れます。qは直行行列${\bf Q}$で、最初は単位行列とします。uは(3)式の${\bf u}$ベクトルを表します。
for k in range(n-1):
# |x|
absx = 0
for i in range(k, n):
absx += r[i][k]**2
absx = np.sqrt(absx)
if absx == 0:
continueforループで、$N-1$回ループを回します。Pythonでは配列要素は0からインデックスが始まることに注意してください。
absxはベクトルのノルム((8)式の$||{\bf a}_k||$)を求めています。 absxが0の場合はその行は計算しないようにします。
# u=x-y
u[k] = r[k][k] + sign(r[k][k]) * absx
absu = u[k]**2
for i in range(k+1, n):
u[i] = r[i][k]
absu += u[i]**2次にハウスホルダー行列を求めるための${\bf u}$ベクトルを求めます。
上述のとおり${\bf y}$ベクトルは、最初の要素が$||{\bf a}_k||$で後はゼロです。この最初の要素の符号は+でも-でもどちらでも構いません。ここでは、数値的に桁落ちが起きないように、$a_{kk}$の要素の符号と逆符号を選び差をとることにします。この符号の選択は
u[k] = r[k][k] + sign(r[k][k]) * absx
のsign関数の部分で行っています。
また、ここでは同時にabsuに$|| {\bf u}||^2$を計算しています。
# sign function
def sign(x):
if x >= 0:
return 1
else:
return -1sign関数はプログラムの冒頭で定義しています。値が0以上なら1、負なら-1を返します。PythonのNumpyにもsign関数はありますが、値が0なら0が返ってしまうので、あえて独自関数を定義しています。
# H=I-2uu'/|u|^2
h = np.eye(n)
for i in range(k, n):
for j in range(k, n):
h[i][j] -= 2 * u[i] * u[j] / absu次に、ハウスホルダー行列hを求めます。最初にeye関数で単位行列としておきます。あとは、(k, k)より右下の行列要素に対して(3)式のとおりハウスホルダー行列を計算します。
r = np.dot(h, r)
q = np.dot(q, h) 最後に(13)、(15)式より${\bf R}$、${\bf Q}$を求めます。
プログラムを実行すると、次のように出力されます。
Q =
[[-0.33333333 0.66666667 -0.66666667]
[-0.66666667 -0.66666667 -0.33333333]
[-0.66666667 0.33333333 0.66666667]]
R =
[[-3.00000000e+00 -9.00000000e+00 -6.00000000e+00]
[-2.22044605e-16 3.00000000e+00 1.20000000e+01]
[ 2.22044605e-16 0.00000000e+00 9.00000000e+00]]
QR =
[[ 1. 5. 4.]
[ 2. 4. -7.]
[ 2. 7. 14.]]${\bf R}$の左下は数値誤差がありますが、ほぼゼロになっています。また、${\bf Q}{\bf R}$は元の${\bf A}$と一致しています。
なお、${\bf Q}$と${\bf R}$の要素の符号をそれぞれ反転させたものも、定義式を満たします。プログラムによっては、${\bf R}$の対角要素をすべて正になるようにとり、一意性を持たせるものもあります。
まとめ
今回は行列のQR分解についてお話しました。当サイトの以下のページでは与えた行列のQR分解ができますので試してみてください。

