【科学技術計算講座ミニ】OpenFOAMにおける行列データ格納方法

以前、疎行列で効率的にデータを格納する方法として圧縮行列格納方式（CRS）について紹介しました。

今回は実際のソフトウェアであるOpenFOAMの行列データ格納方法について見ていきたいと思います。

OpenFOAMとは

OpenFOAMとは皆さんご存知のとおり、フリーでオープンソースの汎用熱流体解析ソフトウェアです。３次元の熱流体解析が無料で出来る優れたソフトです。

使い方は結構めんどうなものの、ソースコードが全てオープンになっているので、やろうと思えばかなり複雑な計算まで独自に開発することができます。

フリーで３次元の流体解析を行いたいという場合は、まずは初めの選択肢となるのではないでしょうか。

※２次元定常熱流体解析であれば、無料で簡単に使える当サイトのオンライン熱流体解析ツールCATCFDzeroもぜひお試しください。

OpenFOAMの行列データ格納方法

OpenFOAMは流体解析ソルバーのため、計算で解かれる行列は疎行列です。疎行列のデータ格納方法には前述の圧縮行列格納方式（CRS）などいろいろな方法がありますが、OpenFOAMでは面に基づいたデータ格納方法が採用されています。

例えば、次のようなメッシュがあったとします。

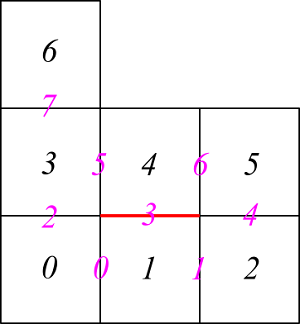
図１

メッシュは０番から６番まで７個のセルで構成されています（黒色がセル番号）。各セルはフェース（面）で隣接していて、その面番号は０番から７番（ピンク色の番号）の番号がついています。

このとき、このセルで構成される方程式の係数行列は次のようになります。

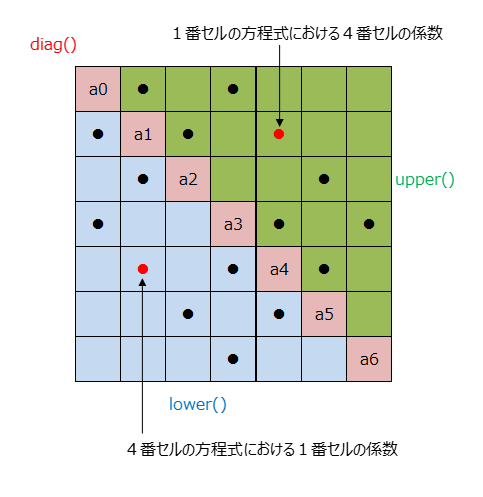
図２

まず行列の対角要素にそのセル自信の係数が並びます。これはセル番号をインデックスに持つ配列diagとして定義されます。

次に非対角要素は下側をlower、上側をupperの三角部分に分けます。この要素はそれぞれ面の数だけ存在します（図の丸点。それ以外の箇所は全てゼロ）。そこで、それぞれの三角部分は面番号をインデックスとした配列の形で係数データを格納します。例えば、図２の赤丸の点は図１の３番の面（赤い面）に対応しています。lower側は、４番セルの方程式における１番セルの係数a41を表しています。そして、upper側は１番セルの方程式における４番セルの係数a14を表します。

ここで、lower、upperだけでは何番のセルに対応しているかわからないため、lowerAddr、upperAddrという２つの配列を用意します。これらも面番号をインデックスとしており、その面を挟んで小さいセル番号をlowerAddrに、大きいセル番号をupperAddrに格納します。赤丸のlowerAddrには１、upperAddrには４が入ります。

なお、面を挟んで小さい番号のセルはownerセル、大きい番号のセルはneighborセルと呼ばれています。

この例では、それぞれの配列には次のようにデータが格納されます。

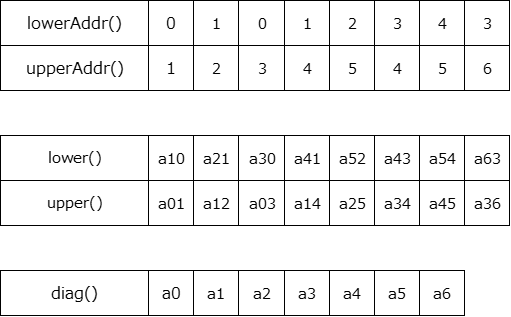
このように、疎行列の非ゼロ要素のみが保持される効率的な方法になっています。

なお、これらはOpenFOAMのlduMatrix、lduAddressingクラスに定義されています。

プログラム例

このデータ格納方式を使って、CRSの時と同様に係数行列${\bf A}$とベクトル${\bf x}$の積

$${\bf A}{\bf x}={\bf b} \tag{1}$$

を求める擬似的なプログラムを書いてみます。OpenFOAMはC++で書かれています。

for (label cellI = 0; cellI < diag().size(); cellI++)
{
    b[cellI] = diag[cellI] * x[cellI];
}

for (label faceI = 0; faceI < lower().size(); faceI++)
{
    b[lowerAddr[faceI]] += upper[faceI] * x[upperAddr[faceI]];
    b[upperAddr[faceI]] += lower[faceI] * x[lowerAddr[faceI]];
}

最初に、対角成分にxを掛けます。これはセル番号でループさせています。

次に面でループさせます。最初のbはlowerAddrのセル番号に対応しており、upper側の要素を掛けて加えています。次のbはupperAddrのセルで、lower側の要素を掛けて加えます。このように面によるループを行うことで、２つの隣接セルそれぞれで和をとっていくことができます。

まとめ

今回はOpenFOAMにおける行列データ格納方式についてご紹介しました。CRSとはまた違ったデータ構造ですが、実際のソフトウェアで使われるデータ構造を知っておくと何かの役にたつかもしれません。また、OpenFOAMはオープンソースであるためソースコードも全て確認することができます。実際のコーディング箇所を確かめてみるとよいでしょう。

全体の目次