今回は対流項の差分スキームのうち2次風上差分と勾配制限についてお話しします。
1次風上差分と中心差分スキームは以下の記事を参照ください。
目次
2次風上差分スキーム
1次風上差分は、面の値を風上のセルの値としました。そこで、もう少し精度よくするため、風上のセルの値$\phi_C$とそのセルの勾配$\nabla \phi_C$を使って求めることにします。
$$\phi_f = \phi_C + \nabla \phi_C \cdot {\bf d}_{Cf} \tag{1}$$
ここで、${\bf d}_{Cf}={\bf x}_f - {\bf x}_C$、$f$:面$e$、$w$
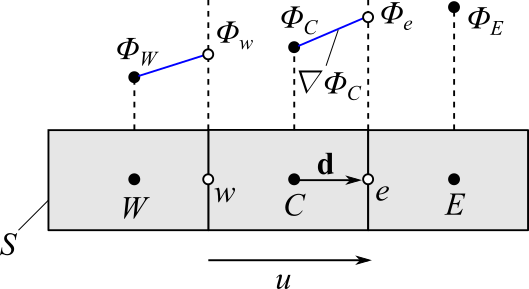
このスキームについても、1次風上差分で行ったように線形方程式の係数を求めてみたいと思います。
(2)式の右辺第一項と第二項は1次の風上差分と同じですが、第三項と第四項は追加の項になっていることが分かります。つまり(2)式は、次のような形をしています。
$$\dot{m}_f \phi_f = \dot{m}_f\phi_f^U + \dot{m}_f \phi_f^{corr} \tag{3}$$
ここで、$\phi_f^U$:1次風上差分の値、$\phi_f^{corr}$:追加の項
線形方程式を作る際に、(3)式の右辺第二項はソース項として扱うことにします。つまり、方程式は次のようになります。
$$a_C \phi_C + a_E \phi_E + a_W \phi_W = b_C \tag{4}$$
ここで、
$$\begin{split} a_E &= \min (\dot{m_e}, 0) \\ a_W &= \min (\dot{m_w}, 0) \\ a_C &= -(a_E + a_W) \\ b_C &= - \{\dot{m}_e \phi_e^{corr} + \dot{m}_w \phi_w^{corr} \} \end{split} \tag{5}$$
左辺の係数$a$は1次風上差分の形になっており、追加の項は右辺のソース項で陽的に与えられます。
(1)式の形で補間するスキームは、2次精度です。したがって、このスキームは、2次風上差分(Second Order Upwind)スキームと呼ばれています。流体解析ソフトによっては、Linear Upwind と呼ばれる場合もあります。
勾配制限
2次風上差分は1次に比べ精度がよく、数値拡散も小さいのですが、数値振動がおこったり、値がまわりのセルに比べて大きくなったり(オーバーシュート)、小さくなったり(アンダーシュート)する現象が起こる場合があります。
そこで、これを抑制するために、(1)式の勾配に制限を設けることがあります。
$$\phi_f = \phi_C + \psi \nabla \phi_C \cdot {\bf d}_{Cf} \tag{6}$$
ここで、$\psi$:勾配制限関数($0 \le \psi \le 1$)
$\psi$が0だと1次風上で、1だと元の2次風上スキームとなります。
$\psi$のとりかたは、さまざまな方法が提唱されていますが、ここではBarth and Jespersonの制限関数[1]をご紹介します。
これは、面の値$\phi_f$が隣接するセルの値を超えないように制限する方法です。
ここで、$\phi_C^{max} = max(\phi_C, \phi_F)$、$\phi_C^{min} = min(\phi_C, \phi_F)$、$\phi_f$は制限を課さない値
勾配制限を付加すると安定性が増すため、よく使われています。
1次、2次風上差分スキームの結果比較
スキームによる解の違いを見てみたいと思います。当サイトのCATCFDzeroを使って、キャビティ流れの結果の違いを見た結果です。
キャビティ流れの詳細は以下のページを参照ください。
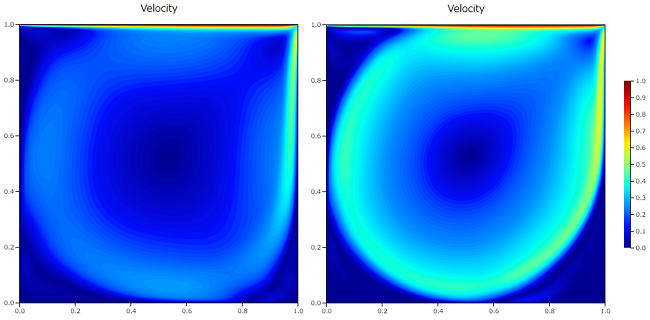
スキームによる速度場の比較(左:1次風上差分、右:2次風上差分)
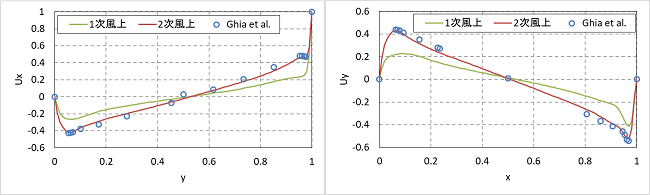
中央線での速度(左:x中央、右:y中央)
この結果を見ると、1次風上差分は数値拡散により解がなまってしまい、文献に比べピーク値が下がっていることが分かります。一方、2次風上差分は速度場がシャープに捉えられ、文献値と一致しています。
まとめ
今回は、2次風上差分スキームの解説を行いました。差分スキームはこの他にも数多くのスキームがあります。
流体解析ソフトによって、どのスキームが標準となっているかは異なります。ただ、一般的には、安定性重視で1次風上差分、精度重視で2次風上差分もしくはそれに準ずる2次精度のスキームが使われることが多いのではないかと思います。
高次精度の場合は、今回紹介した勾配制限などを付加したり、TVDスキームといった別のタイプのスキームが使われる場合もあります。
使用するソフトのマニュアルを見ると、どのようなスキームが使われているか書いてあるはずなので、一度読んでおくとよいと思います。