【科学技術計算講座ミニ】QR法で行列の固有値を求める②

前回、行列の固有値をQR法で求める方法について解説しました。

今回はPythonでQR法のプログラムを作成していきます。

QR法のプログラム

早速ですが全体のプログラムを示しておきます。

import numpy as np

# sign function
def sign(x):
  if x >= 0:
    return 1
  else:
    return -1

# Hessenberg matrix
def hessenberg(a):
  n = a.shape[0]
  r = a.copy()
  u = np.zeros(n)
  for k in range(n-2):
    # |x|
    absx = 0
    for i in range(k+1, n):
      absx += r[i][k]**2
    absx = np.sqrt(absx)
    if absx == 0:
      continue

    # u=x-y
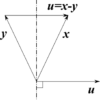
    u[k+1] = r[k+1][k] + sign(r[k+1][k]) * absx
    absu = u[k+1]**2
    for i in range(k+2, n):
      u[i] = r[i][k]
      absu += u[i]**2

    # H=I-2uu'/|u|^2
    h = np.eye(n)
    for i in range(k+1, n):
      for j in range(k+1, n):
        h[i][j] -= 2 * u[i] * u[j]  / absu

    # R=H'RH
    r = np.dot(h, r)
    r = np.dot(r, h)  

  return r    

# QR decomposition for Hessenberg matrix
def qr_decomposition(a):
  n = a.shape[0]
  r = a.copy()
  q = np.eye(n)
  u = np.zeros(n)
  for k in range(n-1):
    # |x|
    absx = 0
    for i in range(k, k+2):
      absx += r[i][k]**2
    absx = np.sqrt(absx)
    if absx == 0:
      continue

    # u=x-y
    u[k] = r[k][k] + sign(r[k][k]) * absx
    u[k+1] = r[k+1][k]
    absu = u[k]**2 + u[k+1]**2

    # H=I-2uu'/|u|^2
    h = np.eye(n)
    for i in range(k, k+2):
      for j in range(k, k+2):
        h[i][j] -= 2 * u[i] * u[j]  / absu

    r = np.dot(h, r)
    q = np.dot(q, h)  

  return q, r    

# Wilkinson shift
def wilkinson_shift(a):
  n = a.shape[0]
  a11 = a[n-2][n-2]
  a12 = a[n-2][n-1]
  a21 = a[n-1][n-2]
  a22 = a[n-1][n-1]
  c1 = a11 + a22
  c2 = np.sqrt((a11 - a22)**2 + 4 * a12 * a21)
  mu1 = 0.5 * (c1 + c2)
  mu2 = 0.5 * (c1 - c2)
  dmu1 = np.abs(a22 - mu1)
  dmu2 = np.abs(a22 - mu2)
  if dmu1 <= dmu2:
    return mu1
  else:
    return mu2  

# input parameter
iter_max = 1000
eps = 1.0e-12

a0 = np.array([[6., -3., 5.], [-1., 4., -5.], [-3., 3., -4.]]) 
n = a0.shape[0]
eigen_value = np.zeros(n)
h = hessenberg(a0)

print("A =\n", a0, "\n")
print("Hessenberg =\n", h, "\n")

#QR method
for k in range(n, 1, -1):
  # deflation
  a = np.zeros((k, k))
  for i in range(k):
    for j in range(k):
      a[i][j] = h[i][j]

  #QR method with Wilkinson shift
  for iter in range(iter_max):
    mu = wilkinson_shift(a)
    for i in range(k):
      a[i][i] -= mu

    q, r = qr_decomposition(a)
    a = np.dot(r, q)

    for i in range(k):
      a[i][i] += mu

    if np.abs(a[k-1][k-2]) < eps:
      eigen_value[k-1] = a[k-1][k-1]
      if k == 2:
        eigen_value[0] = a[0][0]
      h = a.copy()
      break   

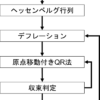
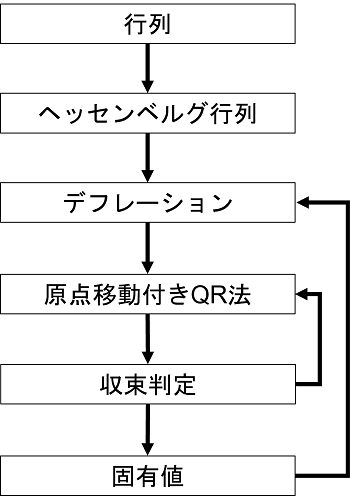
print("Eigenvalue =\n", eigen_value, "\n")

プログラム全体のフローは次のようになっています。

以下プログラムの内容を説明していきますが、QR分解に関する部分は以下のページで詳しく解説しているので要点だけ示します。

ヘッセンベルグ行列

ヘッセンベルグ行列を計算する関数 hessenbergを定義しています。

# Hessenberg matrix
def hessenberg(a):

基本的にはQR分解のコードと同じです。ただし、対角要素の一つ下まで値が入るため行が一つずれていることに注意してください。最後にハウスホルダー行列を右と左から掛け合わせています。

QR分解

QR分解を行う関数 qr_decompositionを定義しています。

# QR decomposition for Hessenberg matrix
def qr_decomposition(a):

以前のQR分解のコードと違うのは、扱う行列がヘッセンベルグ行列であるため、行に対しては対角要素の一つ下の要素までしか演算していないところです。

Wilkinsonの移動法

原点移動法のWilkinsonシフトの関数wilkinson_shiftを定義します。

# Wilkinson shift
def wilkinson_shift(a):
  n = a.shape[0]
  a11 = a[n-2][n-2]
  a12 = a[n-2][n-1]
  a21 = a[n-1][n-2]
  a22 = a[n-1][n-1]
  c1 = a11 + a22
  c2 = np.sqrt((a11 - a22)**2 + 4 * a12 * a21)
  mu1 = 0.5 * (c1 + c2)
  mu2 = 0.5 * (c1 - c2)
  dmu1 = np.abs(a22 - mu1)
  dmu2 = np.abs(a22 - mu2)
  if dmu1 <= dmu2:
    return mu1
  else:
    return mu2

与えられた行列aの右下角の２×２の行列で固有値mu1、mu2を求めます。２次の行列なので２次方程式の解の公式から求めています。このうち右下角の要素a22に近い方の固有値を返しています。

パラメータの入力

計算に必要なパラメータを入力します。

# input parameter
iter_max = 1000
eps = 1.0e-12

a0 = np.array([[6., -3., 5.], [-1., 4., -5.], [-3., 3., -4.]]) 
n = a0.shape[0]
eigen_value = np.zeros(n)
h = hessenberg(a0)

print("A =\n", a0, "\n")
print("Hessenberg =\n", h, "\n")

iter_maxはQR法の繰り返し計算の最大繰り返し数。epsはQR法で要素がゼロになったかどうかの収束判定値。a0は固有値を求める行列。nは行列の次数。eigen_valueは算出された固有値を格納する配列です。

hはa0を変換したヘッセンベルグ行列です。a0とhはprintで出力しています。

QR法

ここからがQR法のメイン部分です。

#QR method
for k in range(n, 1, -1):
  # deflation
  a = np.zeros((k, k))
  for i in range(k):
    for j in range(k):
      a[i][j] = h[i][j]

最終的に、固有値はN個見つかります。１回のステップで、行列の一番右下角に求める固有値が計算されます。固有値が１つ見つかるとデフレーションで行列の次数を減らします。最終的にN-1回目のループで２×２の行列となり、２つの対角成分がそれぞれ固有値なので、全て見つかったことになります。

最初のfor文はN-1回のループで、インデックスkはNから2までループされます。

デフレーションで次数kの行列aを作っています。

  #QR method with Wilkinson shift
  for iter in range(iter_max):
    mu = wilkinson_shift(a)
    for i in range(k):
      a[i][i] -= mu

QR法の繰り返し部分です。先ほど定義したiter_maxまで最大でループされますが、この後出てくる収束判定により途中でループを抜けることになります。

まずmuにWilkinsonシフトで求めた固有値を入れます。そして、対角成分から引きます。

    q, r = qr_decomposition(a)
    a = np.dot(r, q)

    for i in range(k):
      a[i][i] += mu

q、rにQR分解をしたQとRの行列を入れます。そして、それを逆にかけてaとします。最後に対角成分にmuを加えます。これで原点移動付きのQR法の計算になります。

    if np.abs(a[k-1][k-2]) < eps:
      eigen_value[k-1] = a[k-1][k-1]
      if k == 2:
        eigen_value[0] = a[0][0]
      h = a.copy()
      break

最後に収束判定をします。a[k-1][k-2]がepsより小さくゼロになったと判定されれば、QR法が収束したものとみなします。a[k-1][k-2]は行列の一番右下角の一つ左の要素です。今はヘッセンベルグ行列を考えているので、この要素がゼロになれば、最後の行の対角要素以外が全てゼロになったとみなすことができます。

収束すれば、eigen_valueに対角要素a[k-1][k-1]（これが求める固有値）を格納します。k=2のときは２×２行列になったので、a[0][0]も格納してやります。

そして、aをhにコピーしてbreakでループを抜けます。

プログラムの実行結果

プログラムを実行すると、次のように出力されます。

A =
 [[ 6. -3.  5.]
 [-1.  4. -5.]
 [-3.  3. -4.]]

Hessenberg =
 [[ 6.00000000e+00 -3.79473319e+00  4.42718872e+00]
 [ 3.16227766e+00 -3.80000000e+00  5.60000000e+00]
 [-5.55111512e-16 -2.40000000e+00  3.80000000e+00]]

Eigenvalue =
 [3. 2. 1.]

※このプログラムは固有値が複素数になる問題には対応していません。

まとめ

QR法による行列の固有値計算のプログラムをPythonで作成しました。今回は固有値のみを求めましたが、固有ベクトルは別途求める必要があります。固有ベクトルの求め方はまた別の機会にお話しします。

当サイトの以下のページでは行列の固有値を実際に計算することができますので試してみてください。

全体の目次