今回は行列の固有値をQR法で求める方法について解説します。
目次
行列の固有値とは
ある正方行列${\bf A}$をベクトル${\bf x}$に作用させたとき、そのベクトル${\bf A}{\bf x}$がもとのベクトル${\bf x}$の定数倍となる場合、
$${\bf A}{\bf x} = \lambda {\bf x} \qquad ({\bf x} \neq {\bf 0}) \tag{1}$$
$\lambda$をその行列の固有値、${\bf x}$を固有ベクトルといいます。
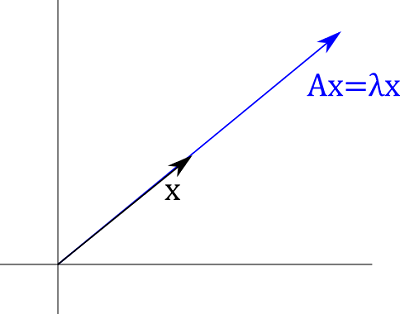
要するに、ベクトルに対してある変換を行ったとき、そのベクトルの長さを変えるような変換を意味しているのですが、このような状況は様々な物理や数学、工学の分野で出てきます。
固有値の求め方は、(1)式より、
$$({\bf A} - \lambda {\bf I}) {\bf x} = {\bf 0} \tag{2}$$
となるので、固有値$\lambda$は、
$$|{\bf A} - \lambda {\bf I}| = 0 \tag{3}$$
の解として求められます。つまり、次の行列式からなる固有方程式
を解くと$\lambda$が求まります。
行列の固有値は、N次正方行列の場合はN個存在します。これは(4)式の行列式は、$\lambda$のN次方程式になることから明らかです。ただし、重複して同じ固有値が複数ある場合があるので、独立した数としてはN個より少ない場合があります。また、固有値が複素数になる場合もあります。
固有値を求めるには(4)式を解けばよいのですが、行列の要素が多い場合、行列式を直接解くことは容易ではないので、別の方法が考えられています。ここではQR法という方法を紹介します。
QR法とは
QR法とは行列のQR分解を使って固有値を求める方法です。QR分解は以下の記事を参照してください。
QR法は次のような方法で固有値を求めます。
行列${\bf A}$をQR分解します。ここで上添え字$k$は繰り返しのステップを表します。
$${\bf A}^{(k)} = {\bf Q}^{(k)} {\bf R}^{(k)} \tag{5}$$
次に、QとRを反対にかけて
$${\bf A}^{(k+1)} = {\bf R}^{(k)}{\bf Q}^{(k)} \tag{6}$$
とします。これを繰り返すと、${\bf A}^{(k)}$は対角成分より下の要素はゼロに収束し、上三角行列の形になることがわかっています。この三角行列の対角成分が行列${\bf A}$の固有値になっています。
変換した行列の固有値がもとの行列の固有値と同じであるのは、(6)式が相似変換になっていることから導かれます。相似変換というのは、
$${\bf B} = {\bf P}^{-1}{\bf A}{\bf P} \tag{7}$$
のような形の変換のことを言います。(6)式は(5)式を用いて書き換えると
となっており相似変換であることがわかります。ここで重要なことは、「相似変換の前後で固有値は変わらない」という性質があることです。つまり、${\bf A}^{(k)}$と${\bf A}^{(k+1)}$の固有値は同じです。
QR法は(5)(6)式を繰り返し行うだけなのでシンプルですが、収束に時間がかかる場合があります。そこで収束を早めるためのいくつかの方法を加えてやります。
ヘッセンベルグ行列
もとの行列をそのままQR法にかけるより、三角行列に近いものを計算した方が計算量を抑えることができます。そこで、最初に行列${\bf A}$をヘッセンベルグ行列(Hessenberg matrix)に変換します。
ヘッセンベルグ行列とは次のように、右上三角行列の対角成分の一つ下の要素まで値が入った行列のことです。
このような、ある要素より下の部分がゼロである行列にするためには、QR分解で用いたハウスホルダー変換${\bf H}$を使うと全く同じように変換できます。このとき、変換後の行列ともとの行列の固有値を変えないためには、相似変換を行う必要があるため、${\bf H}^{-1}{\bf A}{\bf H}$のようにしてやります。
QR分解と同様にこれをN-2回作用させると、
$${\bf B} = {\bf P}^{-1}{\bf A}{\bf P} \tag{10}$$
ここで、${\bf P}={\bf H}^{(1)} {\bf H}^{(2)} \cdots {\bf H}^{(N-2)}$
のように、ヘッセンベルグ行列に変換することができます。
ヘッセンベルグ行列をQR分解すると、行列${\bf Q}$もヘッセンベルグ行列になるという性質があります。さらに、${\bf R}{\bf Q}$もヘッセンベルグ行列です。要するに左下のゼロの要素は変換後もゼロのままなので、この部分にかかる計算量を減らすことができます。
ちなみに、非対称行列はヘッセンベルグ行列になり、対称行列は三重対角行列(対角成分とその上下一つ以外は全てゼロ)に変換されます。
原点移動法
QR法で繰り返し計算を行い対角成分が固有値に近づいてくると、対角成分の左隣の要素はゼロに近づいてきます。すると対角成分との差が大きくなり、なかなかゼロに収束しにくくなります。そこで、ある値$\mu$を対角成分から引いた行列でQR分解を実行します(これを原点移動法といいます)。
$${\bf A}^{(k)} - \mu^{(k)} {\bf I} = {\bf Q}^{(k)} {\bf R}^{(k)} \tag{11}$$
$${\bf A}^{(k+1)} = {\bf R}^{(k)}{\bf Q}^{(k)} + \mu^{(k)} {\bf I} \tag{12}$$
ここで、$\mu^{(k)}$は、行列${\bf A}^{(k)}$の右下角の2×2の行列の固有値のうち、右下角の要素の値に近い方をとります。これをウィルキンソンの移動法(Wilkinson shift)と呼びます。
デフレーション
QR法ではN番目の固有値$\lambda_N$から順に求まります。そこで、N番目の固有値が求まったら行列の次数を一つ減らし、小さくした行列で計算を続けます。これをデフレーション(減次)と呼びます。こうすることで計算量を減らすことができます。
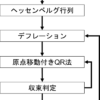
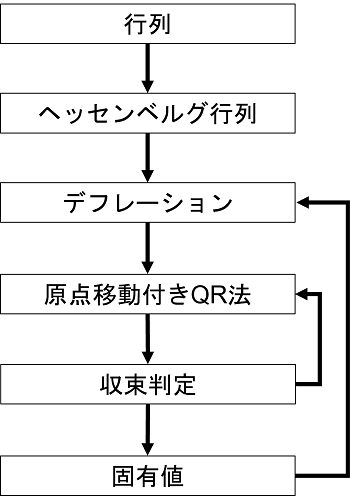
QR法のフロー
ここで紹介した方法のフローを示しておきます。
まとめ
今回は行列の固有値を求める方法の一つであるQR法についてお話しました。
続きは以下のページです。Pythonでプログラム作成を行います。
なお、以下のページでは実際に行列の固有値を計算できるので、試してみてください。