今回は有限体積法の流体解析における対流項の差分スキームについてお話しします。
目次
対流項の離散化
簡単のために、拡散のない定常の移流方程式を考えます。次式のように対流項のみの式となります。
$$\nabla \cdot (\rho \phi {\bf u}) = 0 \tag{1}$$
ここで、$\rho$:密度、$\phi$:物理量、${\bf u}$:流速ベクトル
積分系で表すと、
$$\int_V \nabla \cdot (\rho \phi {\bf u}) dV = 0 \tag{2}$$
となります。ガウスの発散定理より、面積積分にすると、
$$\int_S \rho \phi {\bf u} \cdot d {\bf S} = 0 \tag{3}$$
と変形できます。
面積積分はセルの面$f$の和で表し、次式のようになります。
$$\sum_f (\rho \phi {\bf u})_f \cdot {\bf S}_f = 0 \tag{4}$$
ここで、${\bf S}$:面の面積ベクトル(セルから外に向かう方向が正)
ここで、さらに簡単のために1次元の有限体積メッシュを考えます。
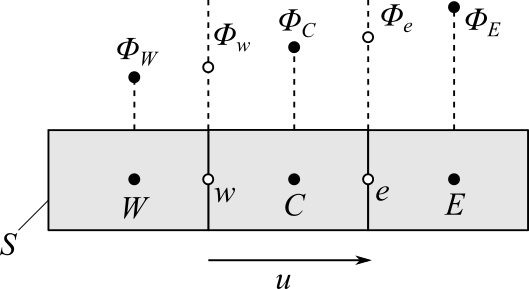
セル$C$について考えると、(4)式は面$e$と面$w$の和となり、
$$(\rho \phi u S)_e - (\rho \phi u S)_w = 0 \tag{5}$$
と書けます。
ここで、面での物理量$\phi$の値が必要になります。面での値をどのように計算するかは、いろいろな方法が考えられます。
風上差分スキーム
まず、面での$\phi$は上流(風上)の値をそのまま使って外挿するという、単純な方法を考えます。物理量は流体に乗って移流してくることを考えれば、風上の値を使うことは理にかなっているといえます。
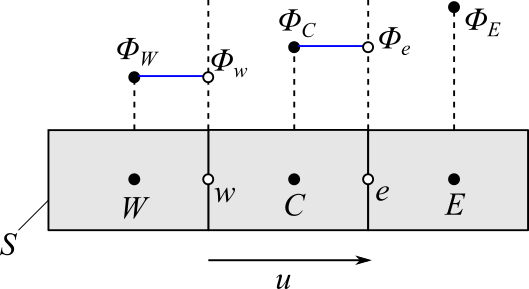
いま、図のように、流体は左から右に一定流速$u$で流れているとします。面$e$を考えると、風上はセル$C$となるので、$\phi_C$が面$e$での値となります。
流速の方向が決まっていなければ一般的に、
$$\phi_e = \begin{equation} \begin{cases} \; \phi_C & \dot{m_e} > 0 \\ \; \phi_E & \dot{m_e} < 0 \end{cases} \end{equation} \tag{6}$$
ここで、$\dot{m_e}=(\rho {\bf u} \cdot {\bf S})_e$:面$e$での質量流束
と書けます。面$w$も同様に、
$$\phi_w = \begin{equation} \begin{cases} \; \phi_C & \dot{m_w} > 0 \\ \; \phi_W & \dot{m_w} < 0 \end{cases} \end{equation} \tag{7}$$
ここで、$\dot{m_w}=(\rho {\bf u} \cdot {\bf S})_w$:面$w$での質量流束
となります。
ここで、(5)式の左辺第一項は、(6)式をひとつの式で書き表して、
と書けます。同様に左辺第二項は、
となります。
(8)、(9)式を(5)式に代入して整理すると、次の線形方程式ができあがります。
$$a_C \phi_C + a_E \phi_E + a_W \phi_W = 0 \tag{10}$$
ここで、
なお、最後の$a_C$の計算には、質量保存$\dot{m_e} + \dot{m_w} = 0$の関係を使用しています。
このスキームは、次数精度は1次となり、1次風上差分(First Order Upwind)スキームと呼ばれています。CFDソフトにより呼び方は異なりますが、単にUpwindと言えばこのスキームのことを指すことが多いようです。
これは、1次精度のため解がなまってしまう(数値拡散が強い)傾向がありますが、数値振動がなく安定に計算できるため、安定性重視で使われるスキームです。
当サイトのオンライン流体解析ツールCATCFDzeroでは、デフォルトのスキームは1次風上差分になっています。
中心差分スキーム
続いて、別の補間方法を考えてみます。面の値を面を挟むセルの値を使って線形補間で表してみます。
$$\phi_e = (1-g_e) \phi_C + g_e \phi_E \tag{12}$$
ここで、$g_e = (x_e - x_C) / (x_E - x_C)$、$x$は位置
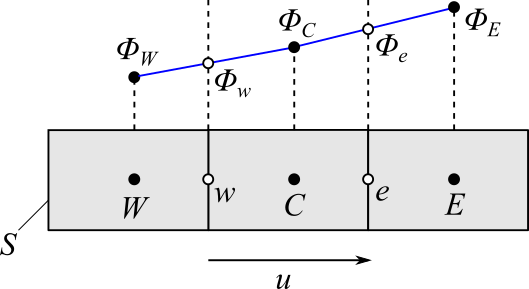
もし、セル幅が一定であれば、単純に
$$\phi_e = \frac{\phi_C + \phi_E}{2} \tag{13}$$
と両サイドの平均値となります。
(11)式と同様に整理すると、
と係数が決まります。
このスキームは、中心差分(Central Difference)スキームと呼ばれています。(ただし、面の値を線形補間で求めることから、OpenFOAMでは linear と表記されています。)
このスキームは2次精度です。精度は高いですが、数値振動が起こりやすく、発散しやすくなることから、通常の流れでは使うことはありません。ただし、LES乱流モデルのように空間精度を重視する場合は、中心差分が使われます。
まとめ
今回は、有限体積法による流体解析で使われる、対流項の差分スキームのうち、風上差分と中心差分について解説しました。
次回は、2次の風上差分と勾配制限、それぞれのスキームの結果の違いについてお話ししたいと思います。
