前回は、境界条件と初期条件の取り扱いについて説明し、Boidモデルのプログラムを完成させました。
今回は本シリーズの最終回です。魚がマウスカーソルに寄ってくるプログラムを作り、インタラクティブなシミュレーションを行ってみます。
目次
マウスカーソルの位置
p5.jsでマウスカーソルの位置は、mouseX、mouseYという変数で簡単に取得できます。
ここで注意ですが、マウスカーソルの位置は、画面のキャンバスの左上が原点となる座標系で、ピクセル単位で表されます。
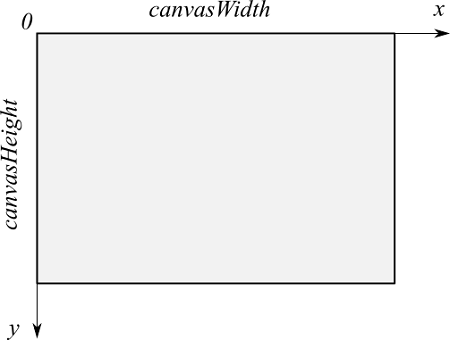
一方、魚の位置は、キャンバスの左下が原点となる座標で計算しています。したがって、マウスカーソルの位置を魚の座標系にするために座標変換してやる必要があります。
const scale = canvasWidth / region.width;
const x = mouseX / scale + region.left;
const y = (canvasHeight - mouseY) / scale + region.bottom;ここでは、x、yがマウスカーソル位置を魚の座標系に変換したものです。
カーソルを追いかける行動規則
魚がカーソルを追いかけるようにするために、Boidモデルの3つの行動規則に新たに行動規則を追加します。
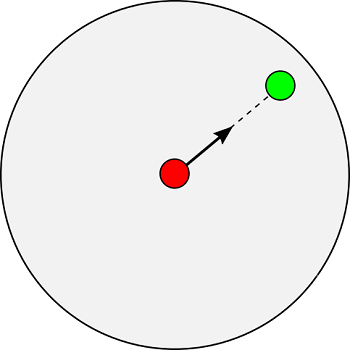
自分の周りの半径$r_{tg}$の円内にカーソル(図の緑丸)があると、その方向に移動する力${\bf F}_{tg}$を受けるとします。
$${\bf F}_{tg} = {\bf P}_{tg} - {\bf P}_i \tag{6-1}$$
ここで、${\bf P}_{tg}$は、カーソルの位置ベクトル。
この力は他の行動規則と同様に、重み係数をかけて合成されます。
プログラムは、particleForce関数内で計算します。
function particleForce() {
const scale = canvasWidth / region.width;
const x = mouseX / scale + region.left;
const y = (canvasHeight - mouseY) / scale + region.bottom;
const target = new Vector(x, y)
for (let i = 0, n = p.length; i < n; i++) {
if (!p[i].active) continue;
let forceSeparation = new Vector();
let forceAlignment = new Vector();
let forceCohesion = new Vector();
let forceTarget = new Vector();
let velAlignment = new Vector();
let vecTarget = new Vector();
let center = new Vector();
let numAlignment = 0, numCohesion = 0;
p[i].forNeighbor(cell, function(pNeighbor, rv) {
if (p[i] !== pNeighbor) {
const r = rv.magnitude();
// separation force
if (r > 0 && r <= radiusSeparation) {
forceSeparation.x += rv.x / (r * r);
forceSeparation.y += rv.y / (r * r);
}
// alignment force
if (r <= radiusAlignment) {
velAlignment.x += pNeighbor.velocity.x;
velAlignment.y += pNeighbor.velocity.y;
numAlignment++
}
// cohesion force
if (r <= radiusCohesion) {
center.x += pNeighbor.position.x;
center.y += pNeighbor.position.y;
numCohesion++;
}
}
});
if (numAlignment > 0) {
velAlignment.x /= numAlignment;
velAlignment.y /= numAlignment;
forceAlignment = velAlignment.sub(p[i].velocity);
}
if (numCohesion > 0) {
center.x /= numCohesion;
center.y /= numCohesion;
forceCohesion = center.sub(p[i].position);
}
// target force
if ((target.x > region.left && target.x < region.right) &&
(target.y > region.bottom && target.y < region.top)) {
vecTarget = target.sub(p[i].position);
const mag = vecTarget.magnitude();
if (mag <= radiusTarget) {
forceTarget.x = vecTarget.x;
forceTarget.y = vecTarget.y;
}
}
// update
forceSeparation.unit();
forceAlignment.unit();
forceCohesion.unit();
forceTarget.unit();
p[i].force.x = wSeparation * forceSeparation.x + wAlignment * forceAlignment.x + wCohesion * forceCohesion.x + wTarget * forceTarget.x;
p[i].force.y = wSeparation * forceSeparation.y + wAlignment * forceAlignment.y + wCohesion * forceCohesion.y + wTarget * forceTarget.y;
}
}先頭で、前述の座標変換を行いマウスカーソルの位置をtargetというベクトル変数に格納しています。
// target force
if ((target.x > region.left && target.x < region.right) &&
(target.y > region.bottom && target.y < region.top)) {
vecTarget = target.sub(p[i].position);
const mag = vecTarget.magnitude();
if (mag <= radiusTarget) {
forceTarget.x = vecTarget.x;
forceTarget.y = vecTarget.y;
}
}この部分でカーソルに寄っていく力を計算しています。なお、カーソルが魚の領域regionの内側にある場合のみ追いかけるようにif文で制御しています。
シミュレーションプログラムのソースコード
あとは、半径radiusTargetや重み係数wTargetの定義を追加するだけです。こちらも、ソースコードをGitHubにアップしておきますので、参考にしてみてください。
→プログラムはこちら(GitHub)
※targetのフォルダを参照してください。
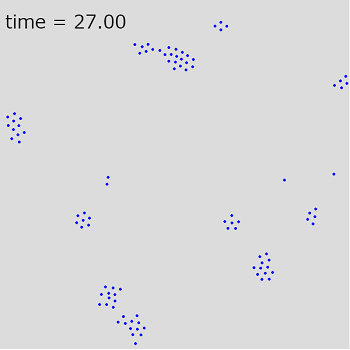
カーソルを領域の中に入れて動かすと、それを追いかけるように魚が寄ってきます。マウスを人間が動かすことにより、バーチャルな魚が行動してくれるという、インタラクティブなシミュレーションができます。これを応用すれば、簡単なゲームも作れそうですね。
まとめ
本シリーズでは、Boidモデルを使って魚の群れをシミュレーションするプログラムを作成しました。単純な行動規則だけで、群れを再現したり、全体として規則的な行動をするようになったり、面白いシミュレーションができます。
また今回は、以前作った粒子法のプログラムをほぼ踏襲して、全然別のシミュレーションを行うことができました。このように色々なシミュレーションの経験があると様々な分野に応用することができて役立ちます。他にも応用できるものがあるか考えてみてください。

