前回はシミュレーションのもとになるBoid(ボイド)モデルについて簡単に説明しました。
今回はBoidモデルの行動規則を数式で表しておきたいと思います。
目次
3つの行動規則
Boidモデルで個体一つ一つの行動は3つの規則がもとになっていると前回お話ししました。プログラムを作成するためには、これらの規則を数式で表しておく必要があります。
まず、ここでは2次元を考えます。魚は2次元平面内を移動するものとします。
分離(Separation)
魚は自分の近くにいる別の魚と離れようとします。これは他の魚と衝突しないようにするための行動です。
これを数式で表すために、以下のようなモデルを考えます。赤丸の魚に着目すると、自分の周りの半径$r_s$の円内にいる他の魚(青丸)から離れようとします。つまり、他の魚の位置から自分の位置に引いたベクトル方向に離れて行けばよいです。これは、斥力のようなイメージです(同じ極の磁石を近づけると働く反発力をイメージしてください)。円内に複数の魚がいる場合は、そのベクトルを合成した方向に移動することにします。
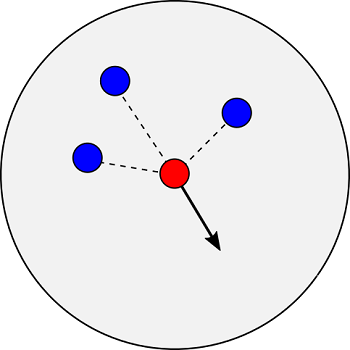
また、遠くにいる魚より近くにいる魚の影響をより強く受けるため、他の魚と自分との間の距離の2乗で割って合成することにします。ここで、赤の魚を$i$、青の魚を$j$の添字とすると、分離により魚$i$が行動する方向(力の方向)${\bf F}_s$は、次式のようになります。
$${\bf F}_s = \sum_j \frac{{\bf P}_i - {\bf P}_j}{|{\bf P}_i - {\bf P}_j|^2} \tag{2-1}$$
ここで、${\bf P}$は魚の位置ベクトル。
整列(Alignment)
魚は自分の近くにいる群れと同じ方向に進もうとします。これは、群れが進む方向に自分も進むという規則で表現できます。
魚は自分の周り半径$r_a$の円内にいる群れに合わせて進むとします。群れの進む向きは、青丸の魚の進行方向(速度ベクトルの方向)を平均した向きとします。
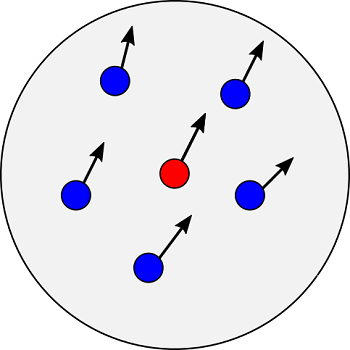
つまり群れの速度${\bf v}_a$は、
$${\bf v}_a = \frac{\sum_j {\bf v}_j}{N_a} \tag{2-2}$$
と表せます。$N_a$は、群れの中にいる他の魚の数。
この速度の向きに自分の速度の向きを合わせるため、魚$i$の移動方向(魚にかかる力)${\bf F}_a$は、以下のようになります。
$${\bf F}_a = {\bf v}_a - {\bf v}_i \tag{2-3}$$
結合(Cohesion)
魚は自分の近くにいる群れの中心に集まろうとします。群れようとする習性を表すためのものです。
これは、自分の周りの半径$r_c$の円内にいる他の魚が作る群れの中心位置に向かって力が働き、移動するとモデル化できます。
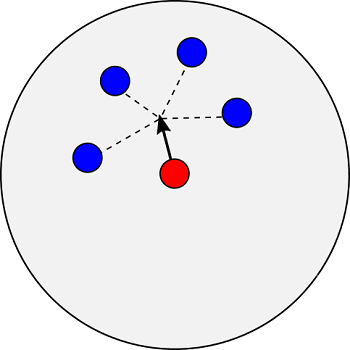
他の魚の群れの中心${\bf P}_c$は、
$${\bf P}_c = \frac{\sum_j {\bf P}_j}{N_c} \tag{2-4}$$
で計算できます。ここで$N_c$は、この群れの中にいる他の魚の数。
魚$i$は、この中心位置に向かって移動しようとするため、魚$i$にかかる力(移動方向)${\bf F}_c$は次式で表せます。
$${\bf F}_c = {\bf P}_c - {\bf P}_i \tag{2-5}$$
移動速度と位置の更新
力の合成
3つの行動規則による力の方向(移動方向)がわかりました。それぞれの移動方向は、個別に計算されます。では、最終的な移動方向はどのように計算すればよいでしょうか。
ここでは、3つの方向に重み係数をかけて足し合わせることにより、移動方向を決定することにします。今、それぞれの力にかかる重み係数を$w$とし、力を合成します。ただし、力の大きさのスケールがそれぞれ異なるので、ここではわかりやすくするため、各力ベクトル${\bf F}$を単位ベクトル${\bf \tilde F}$にして足し合わせることにします。つまり、合力${\bf F}_t$は、
$${\bf F}_t = w_s {\bf \tilde F}_s + w_a {\bf \tilde F}_a + w_c {\bf \tilde F}_c \tag{2-6}$$
で計算します。
こうすると、重み係数が大きいと、その行動が優位に働きます。逆に、重み係数が他に比べて小さいと、その行動規則にはあまり影響されないことになります。
速度の更新
力が求まったので魚の移動速度${\bf V}$は、次式で計算します。
$${\bf V}^{n+1} = {\bf V}^{n} + {\bf F}_t \Delta t \tag{2-7}$$
ここで、$n$は時間ステップ、$\Delta t $は時間刻みを表しています。
位置の更新
速度が求まると、次式で位置が計算できます。
$${\bf P}^{n+1} = {\bf P}^{n} + {\bf V}^{n+1} \Delta t \tag{2-8}$$
これをすべての魚に対して個別に計算していきます。
なお、文献によって各項や時間発展のさせ方は微妙に違いがあるので、ここで示したのはあくまで一例とお考えください。
まとめ
Boidモデルの行動規則を数式で表しました。各規則は、それほど難しい式ではありませんが、個別に計算された個体が集まると、全体として面白い動きが計算されます。
次回からは、このモデルをプログラミングしていきたいと思います。

