
みんな、こんにちは。
ねこ先生だよ。今日は流体の式についてのお話しだよ。
目次
流体の式
みんな、算数は好きかな? えっ、きらい?
算数はとっても面白いんだけどね。ねこ先生は算数すきだよ。
今日はちょっとだけ算数の話をするね。
流体シミュレーションは、流体がどんなふうに流れるかをコンピュータで計算してるんだったね。計算するっていうことは、何か算数の式があるはずだ。
実は流体の式は、次のような式なんだ。
(1)の式は連続の式といって、流体の質量に関係した式だ。(2)の式はナビエ=ストークス方程式っていう式で、流体の速さに関する式なんだ。
何だかとっても難しそうな式だけど、今日は説明しないから安心してね。この式は大学生で習うから、今は詳しく知らなくてもオッケーだよ。
流体の式って何だかむずかしそうだね。
保存の法則ってなんだ?
今日は流体の式の元になっている考え方についてお話ししよう。この式のもとになっているのは保存の法則(ほぞんのほうそく)と呼ばれるものなんだ。
りんごの数はいくつ?
ここからは、りんごを使って説明してみるね。
箱の中にりんごが1個あるとしよう。

りんごは勝手に増えたり、減ったりしないよね(だれも食べたりしなければ)。だから、何もしなければ箱の中のりんごは1個のままだ。
問題1
この箱の中に新しくりんごを1個入れるとする。箱の中のりんごはいくつになるでしょう?
これは簡単だね。
$$1+1=2$$
答えは2個になる。
問題2
じゃあ、りんごをどんどん箱の中に入れていくとどうなるだろう?
箱の中のりんごの数はどんどん増えていくね。
問題3
こんどは、箱にりんごを1個入れたら、1個りんごを取り出そう。箱の中のりんごの数はどうなる?

はじめにりんごが1個入っていた。新しく1個りんごを入れて、りんごを1個取り出す。
$$1+1-1=1$$
箱の中のりんごは1個だね。1個入れて、1個出すわけだから、箱のりんごの数は変わらないね。このように、数が変わらないようすをりんごの数は保存しているというんだ。
保存とは、「そのままの状態に保っておくこと」っていう意味だ。箱の中のりんごの数はそのままの状態に保たれて変わらないので、保存しているわけだね。
つまり、入れた数と出した数が同じであれば、箱の中の数は保存して変わらない。このように数が保存されていることを保存の法則っていうんだ。
箱を並べた場合
じゃあ次、箱を3つ並べてみよう。はじめ、箱にはそれぞれ1個ずつりんごが入っているとしよう。

いま、左の箱にりんごを新しく1個入れるよ。そしたら、その箱から1個をとなりの箱に移す。となりの箱からも、またとなりの箱に1個移す。最後の箱からは、1個取り出そう。
そうすると、箱の中のりんごの数はどうなってるだろう?
そうだね。箱の中のりんごの数は、それぞれ1個のままだ。つまり、りんごの数は保存されてるわけだね。
これを図で簡単にあらわすと次のようになる。

点線の四角が箱だね。矢印はとなりの箱から入ってくる数を表している。左はしは入り口で、右はしは出口だ。
これ何だか、この前やった流体シミュレーションに似てないかい?
入り口から入って出口から出ていくっていう、流体の流れを矢印で表してたよね。
そう、流体も保存の法則がなりたっているんだ。つまり、箱の中で流体が勝手に増えたり減ったりしなければ、箱に入った流体の量と出ていった流体の量が同じになり箱の中の量は保存される。
流体も保存の法則がなりたってるんだ。
流体シミュレーションの計算の仕方
ここで、この前やった流体シミュレーションを思い出してみよう。領域の左に入り口があって、右に出口があるやつだ。
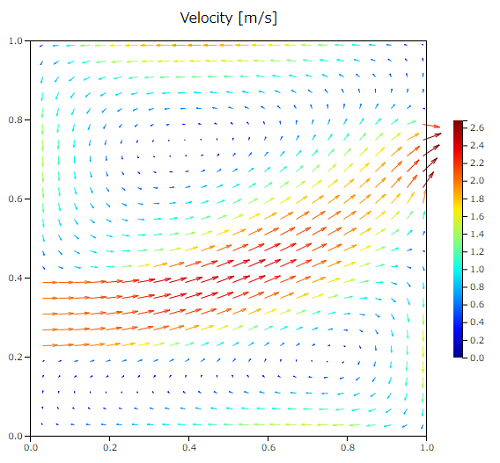
さっきみたいに、この領域の中に小さな箱を置いてみよう。ここでは、領域に9つの箱を置いてみるよ。
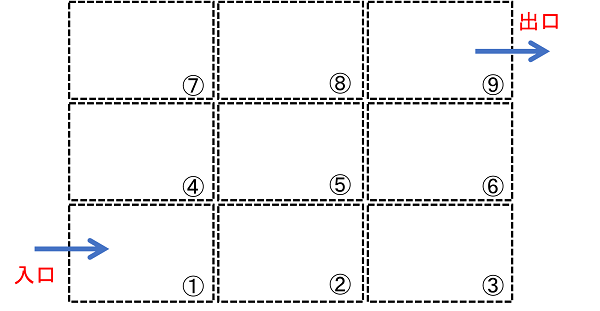
箱①の左の面に入り口があって、箱⑨の右の面に出口があるとしよう。それぞれの箱の流体は、となりの箱に移動することができるよ。
いま、入り口から10の量の流体が入ってくるとするね。保存するためには、箱に入ってきた量と出ていった量が同じになってなくちゃならない。例えば次のような感じだ。
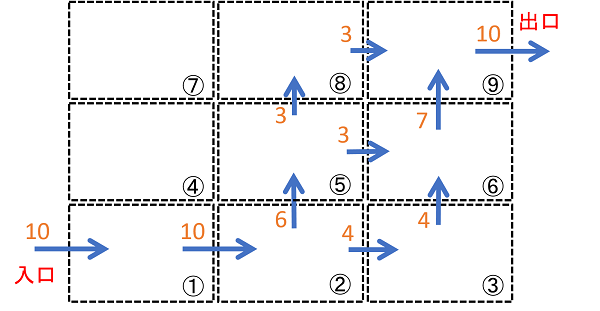
箱①へは10入ってくる。①から②へは同じ10出ていく。入ってくる量と出ていく量が同じなので保存しているね。
箱②はどうだろう、①から10入ってくる。③へは4、⑤へは6出ていってる。出ていく量の合計は10なので、入ってくる量と同じで保存している。
箱⑨を見てみよう、入ってくる量は⑥から7、⑧から3だね。右はしに出口があって、入ってきた量の合計と同じ10が出ていってる。これも保存してるね。
同じように、すべての箱で、入ってきた量の合計と出ていった量の合計が同じになっていて、保存していることがわかる。
これを見ると、入り口から入った流体が、となり合う箱に流体を渡して行きながら、だんだん出口へ向かっているようすがわかるね。
実は、これが流体シミュレーションなんだ。流体シミュレーションは、まず領域を小さな箱に分ける。次にその箱に入ってきた流体の量が、どれだけとなりの箱に移動するかを計算する。これは保存の法則により(1)(2)の式を計算して求めることができる。
- 領域を小さな箱に分ける。
- 保存の法則をもとに、となりの箱に移動する量を計算する。
この前の流体シミュレーションでは小さな箱は見えなかったけど、本当は領域を箱に分けて計算していたんだ。この前の計算では2,500個の箱に分けて計算していたんだよ。
この分ける箱の数が多いと、とても計算の量が多くなって、計算が終わるまでにものすごく時間がかかるんだ。だから、この前話したスーパーコンピュータなんていう大きなコンピュータで計算する必要がある。例えば、1億個みたいなとっても多くの数の箱に分けて計算することもあるんだよ。
箱の数が多いと計算はとても大変なんだけど、流れの細かなようすがよく分かるようになるんだ。
流体シミュレーションって、こんなふうに計算してたんだね。
まとめ
今日はいきなり難しい式が出てきてびっくりしたね。でも、流体シミュレーションって、領域を小さな箱に分けて保存の法則っていうのから計算してたんだね。ちょっと難しかったかもしれないけど、どうだったかな?
さて次回は、また流体シミュレーションをやってみよう。今度はみんなの部屋の中の空気の流れを計算してみるよ。お楽しみに。
次回は、部屋の空気の流れのシミュレーションだ。
