運動方程式シミュレーションツールマニュアル

利用環境

Internet Explorerには対応していません。Google Chrome、Microsoft Edgeなどのブラウザをご使用ください。スマートフォンでの利用は推奨しません。パソコンでご利用ください。
入力された条件や計算結果などは、外部のサーバーには送信されません。計算はすべて、ご使用のパソコン上で行われます。

ツール概要

入力した任意の運動方程式を解くことができます。２次元で３物体までの運動をシミュレーションできます。

運動方程式は４次のRunge-Kutta（ルンゲ=クッタ）法または、Runge-Kutta-Fehlberg法によって解かれます。

使用方法

１．時間のパラメータ入力

時間に関するパラメータを入力します。

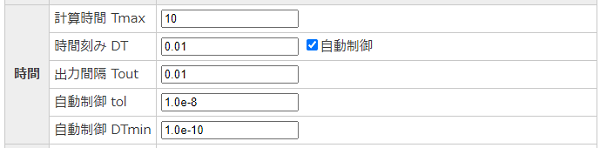
計算時間 Tmax：計算する時間を入力します。
時間刻み DT：時間刻みを入力します。自動制御の場合は、最大の時間刻みになります。
自動制御：チェックを入れるとRunge-Kutta-Fehlberg法により、時間刻みを自動制御して解きます。チェックを外すと時間刻み固定の４次のRunge-Kutta法で解きます。
出力間隔 Tout：出力間隔を指定します。この間隔でグラフやデータが作成されます。
自動制御 tol：時間刻み自動制御に使われる誤差評価のトレランスです。
自動制御 DTmin：時間刻み自動制御での最小の時間刻みです。

２．物体の条件入力

物体の条件を入力します。

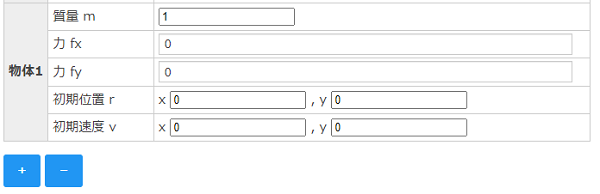
質量 m：物体の質量を入力します。
力 fx：x方向に働く力を入力します。入力方法はこちら
力 fy：y方向に働く力を入力します。
初期位置 r：初期位置 x、yを入力します。
初期速度 v：初期速度 vx、vyを入力します。
[+]ボタン：ボタンを押すと物体が追加されます。最大３つまで。
[-]ボタン：ボタンを押すと物体が削除されます。

３．計算実行

[計算実行]ボタンを押すと計算が実行されます。計算実行中は進捗バーが進行します。時間Tmaxに達すると計算が終了します。

途中で計算を停止する場合は、[計算停止]ボタンを押してください。

４．結果出力

計算が終了すると、結果のグラフが出力されます。

グラフ種類：グラフは、時系列グラフ（Time - xなど）、座標グラフ（x - y）、アニメ（x - y）から選択できます。
x, y：位置座標、r：原点からの距離、vx, vy：速度のx, y成分、vmag：速度の大きさ、fx, fy：力のx, y成分、px, py：ユーザー定義変数
グラフ軸：グラフの軸の最小、最大、刻み、ラベルを指定できます。指定しない場合は自動で調整されます。
グラフにカーソルを合わせると、その位置のデータが表示されます。
グラフの下の凡例をクリックすると、表示/非表示を切り替えることができます。

グラフの設定を変更した場合は、[グラフ表示]ボタンを押すと反映されます。

結果表示用のユーザー変数を定義することができます。

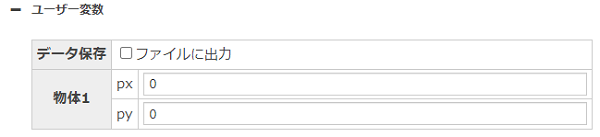
データ保存：チェックを入れると、ユーザー変数がデータ保存のファイル出力時に追加されます。
px、py：ユーザー変数を入力します。入力形式は力と同じです。計算した変数を変換して出力したいときに使います。

アニメ表示は、[アニメオプション]で設定できます。

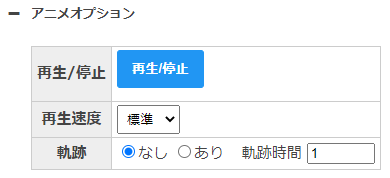
再生/停止：アニメを再生、停止します。最初から再生する場合は[グラフ表示]ボタンを押してください。
再生速度：アニメの再生速度を変更できます。
軌跡：[あり]を選択すると、物体の軌跡をアニメに追加します。軌跡の長さは[軌跡時間]で調整できます。指定した時間前から現在位置までの軌跡が表示されます。

結果データをファイルに保存することができます。

[画像保存]ボタン：グラフの画像をpngファイルに保存します。ファイル名はgraph.pngで通常ダウンロードフォルダに保存されます。
[結果データ保存]ボタン：結果データ（時間t、位置x, y、速度vx, vy、力fx, fy、ユーザー変数px, py）がCSVファイルに保存されます。ファイル名はdata.csvで、ダウンロードフォルダに保存されます。

力の入力方法

使用できる変数は以下のとおりです。

変数	入力形式
時間 t	t
物体の位置座標 x	x[1]　　[]内は物体番号
物体の位置座標 y	y[1]　　[]内は物体番号
原点から物体までの距離 r	r[1]　　[]内は物体番号
物体間の距離 dr	dr[1][2]　　[]内は物体番号。２つの物体番号を指定
物体の速度 vx	vx[1]　　[]内は物体番号
物体の速度 vy	vy[1]　　[]内は物体番号
物体の速度の大きさ vmag	vmag[1]　　[]内は物体番号
物体間の相対速度の大きさ dv	dv[1][2]　　[]内は物体番号。２つの物体番号を指定

※x、yは位置座標としていますが、変位や角度など問題に応じて読み替えてください。

使用できる演算子、数学関数、定数は以下のとおりです。

数式	名称	入力形式
$+$	加算	+
$-$	減算	-
$\times$	乗算	*
$\div$	除算	/
$( )$	括弧	( )
$x^a$	べき乗	x^a
$\sin x$	正弦	sin(x)
$\cos x$	余弦	cos(x)
$\tan x$	正接	tan(x)
$\sin^{-1} x$	逆正弦	asin(x)
$\cos^{-1} x$	逆余弦	acos(x)
$\tan^{-1} x$	逆正接	atan(x)
$\sinh x$	双曲正弦	sinh(x)
$\cosh x$	双曲余弦	cosh(x)
$\tanh x$	双曲正接	tanh(x)

数式	名称	入力形式
$\sinh^{-1} x$	逆双曲正弦	asinh(x)
$\cosh^{-1} x$	逆双曲余弦	acosh(x)
$\tanh^{-1} x$	逆双曲正接	atanh(x)
$e^x$	指数関数	exp(x)
$\ln{x}$	自然対数	log(x)
$\log_{10} x$	常用対数	log10(x)
$\sqrt{x}$	平方根	sqrt(x)
$\|x\|$	絶対値	abs(x)
$\mathrm{sgn} \ x$	符号関数	sign(x)
$\mathrm{\Gamma}(x)$	ガンマ関数	gamma(x)
$\mathrm{B}(a, b)$	ベータ関数	beta(a,b)
$\mathrm{erf}(x)$	誤差関数	erf(x)
$\mathrm{max} \{a, b\}$	最大値	max(a,b)
$\mathrm{min} \{a, b\}$	最小値	min(a,b)
$\pi$	円周率	pi
$g$	重力加速度	g

※必ず半角で入力してください。
※乗算記号は省略できません。例）$2 \pi$ → 2*pi
※重力加速度は、9.80665 [m/s²]です。

例題

いくつか計算の具体例を示します。

空気抵抗のあるボールの軌道

空気抵抗がある場合の投げ上げたボール（球）の軌道を計算します。

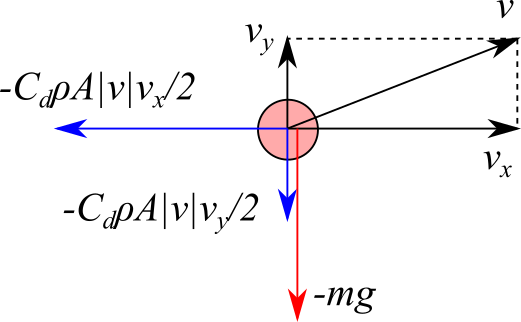
ボールの運動方程式は次式とします。

$$m \frac{d v_x}{d t} = -\frac{1}{2} C_d \rho A |{\bf v}| v_x $$

$$m \frac{d v_y}{d t} = -\frac{1}{2} C_d \rho A |{\bf v}| v_y - m g $$

ここでは、球の質量$m=0.05[kg]$、抗力係数$C_d=0.45$、空気密度$\rho=1.2[kg/m^3]$、球の直径$d=0.05[m]$とします。

球の投影面積$A=\pi d^2/4$なので、$C_d \rho A=0.00106$と計算できます。また、初期条件は、原点から、初速度$v_x=20[m/s]$、$v_y=20[m/s]$で投げるものとします。

したがって、入力は次のようになります。

物体1	質量 m	0.05
	力 fx	-0.50.00106vmag[1]*vx[1]
	力 fy	-0.50.00106vmag[1]vy[1]-m[1]g
	初期位置 r	x 0, y 0
	初期速度 v	x 20, y 20

計算時間Tmaxを4[s]として計算すると、次のような軌道を描きます。

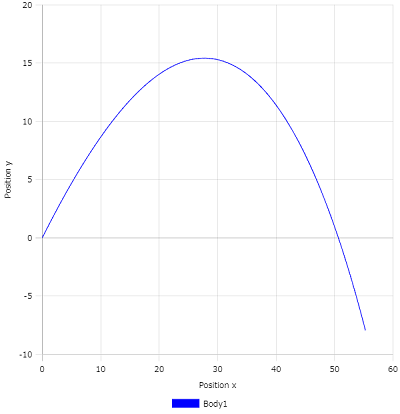
x-yグラフ

連成振動

図のように２つの物体がバネで接続されている場合の振動の様子をシミュレーションしてみます。

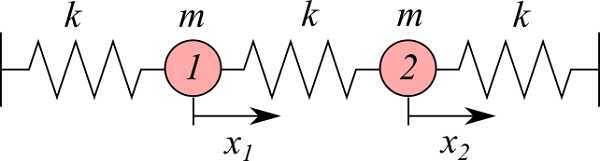
物体の運動方程式は１次元系で、次のようになります。

$$m_1 \frac{d^2 x_1}{d t^2} = -k x_1 + k (x_2 - x_1)$$

$$m_2 \frac{d^2 x_2}{d t^2} = -k (x_2 - x_1) - k x_2 $$

ここで、$x_1$、$x_2$はつり合い位置からの変位とし、バネ定数$k$は全て同じとしています。

条件として、物体の質量$m_1=m_2=2$、バネ定数$k=4$、初期変位$x_1=0$、$x_2=0.5$、初期速度は０とします。

この場合、入力は次のようになります。

物体1	質量 m	2
	力 fx	-4x[1]+4(x[2]-x[1])
	力 fy	0
	初期位置 r	x 0, y 0
	初期速度 v	x 0, y 0
物体2	質量 m	2
	力 fx	-4(x[2]-x[1])-4x[2]
	力 fy	0
	初期位置 r	x 0.5, y 0
	初期速度 v	x 0, y 0

計算時間Tmaxを10として計算すると、変位は次のような時間変化をします。

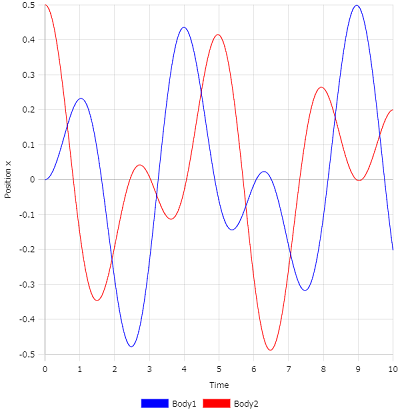
Time-xグラフ

xはつり合い位置からの変位を表すため、表示用に位置座標に変換します。つり合い位置は、物体１は$x=1$、物体２は$x=2$とします。

ユーザー変数に位置座標を定義します。

物体1	px	x[1]+1
物体1	py	0
物体2	px	x[2]+2
物体2	py	0

Time-pxのグラフを表示すると、定義した位置座標の時間変化を確認することができます。

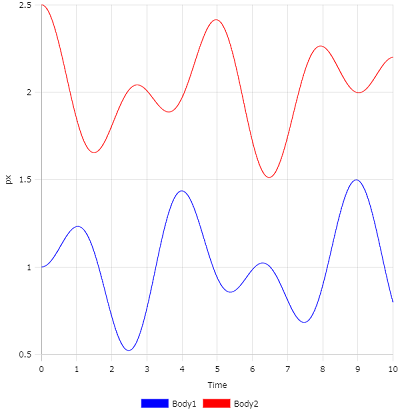
Time-pxグラフ

ピタゴラスの三体問題

３つの物体が重力を及ぼしあって運動する問題を三体問題といいます。

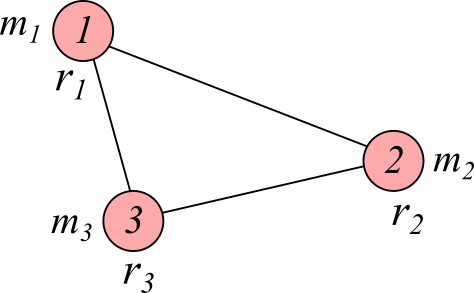
ピタゴラス（またはBurrau）の三体問題とは、初期に各物体が直角三角形の頂点に置かれている場合の軌道を計算する問題です。

規格化された運動方程式は

$$m_i \frac{d^2 {\bf r}_i}{d t^2} = - \sum_{j \ne i} m_i m_j \frac{{\bf r}_i - {\bf r}_j}{|{\bf r}_i - {\bf r}_j|^3} $$

ここで、${\bf r}_i$：物体$i$の位置ベクトル

となります。

初期位置は、下図のような直角三角形の頂点に位置し、初速は０です。

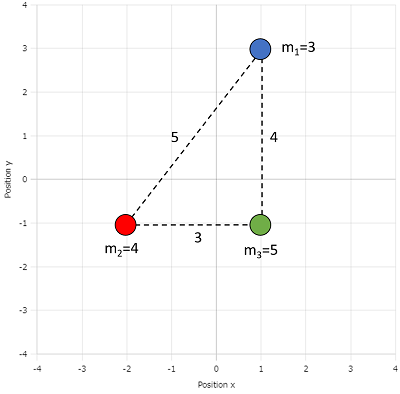
入力は次のようになります。

物体1	質量 m	3
	力 fx	-m[1]m[2](x[1]-x[2])/dr[1][2]^3-m[1]m[3](x[1]-x[3])/dr[1][3]^3
	力 fy	-m[1]m[2](y[1]-y[2])/dr[1][2]^3-m[1]m[3](y[1]-y[3])/dr[1][3]^3
	初期位置 r	x 1, y 3
	初期速度 v	x 0, y 0
物体2	質量 m	4
	力 fx	-m[2]m[1](x[2]-x[1])/dr[2][1]^3-m[2]m[3](x[2]-x[3])/dr[2][3]^3
	力 fy	-m[2]m[1](y[2]-y[1])/dr[2][1]^3-m[2]m[3](y[2]-y[3])/dr[2][3]^3
	初期位置 r	x -2, y -1
	初期速度 v	x 0, y 0
物体3	質量 m	5
	力 fx	-m[3]m[1](x[3]-x[1])/dr[3][1]^3-m[3]m[2](x[3]-x[2])/dr[3][2]^3
	力 fy	-m[3]m[1](y[3]-y[1])/dr[3][1]^3-m[3]m[2](y[3]-y[2])/dr[3][2]^3
	初期位置 r	x 1, y -1
	初期速度 v	x 0, y 0

計算時間Tmaxを70とし、時間刻みの自動制御オプションにチェックを入れます（デフォルトではチェックが入っています）。

計算すると、軌道は次のようになります。

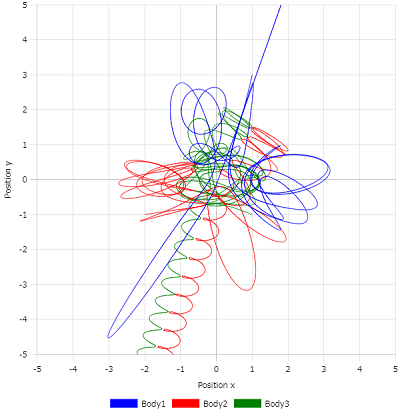
x-yグラフ

また、アニメは次のような軌跡を描きます。

複雑な運動ですが、これは文献[1]と同等の結果になっています。なお、時間刻みの自動制御がない場合は、計算が破綻しうまく計算できません。

また、文献[2]のような高次精度の数値に、ある程度一致させるためには、時間刻みDTを0.00001程度に下げる必要があります（少し計算時間がかかります）。

参考文献[1]：Szebehely, V.; Peters, C. F. Complete Solution of a General Problem of Three Bodies. The Astronomical Journal. 1967, vol. 72, no. 7, p. 876-883.
参考文献[2]：平山弘. ピタゴラス三体問題の４倍精度高次Taylor展開法による数値計算. 情報処理学会研究報告. 2018, vol. 2018-HPC-164, no. 1.

ローレンツ方程式

このツールでは運動方程式だけでなく、１階の連立微分方程式も解くことができます。ここでは次のようなローレンツ方程式を考えます。

$$\frac{d x}{d t} = -p x + p y$$

$$\frac{d y}{d t} = -x z + r x - y$$

$$\frac{d z}{d t} = x y - b z$$

この式は、カオス的な挙動を示すことで知られています。

１階の微分方程式の場合、ツールの速度vxを方程式の$x, y, z$とみなし、解きます。ツールの位置xは無視します。

つまり、$x$ → vx[1]、$y$ → vx[2]、$z$ → vx[3] とします。

条件として、$p=10$、$r=28$、$b=8/3$、初期値を$(x,y,z)=(1,1,1)$とすると、ツールへは次のように入力します。

物体1	質量 m	1
	力 fx	-10vx[1]+10vx[2]
	力 fy	0
	初期位置 r	x 0, y 0
	初期速度 v	x 1, y 0
物体2	質量 m	1
	力 fx	-vx[1]vx[3]+28vx[1]-vx[2]
	力 fy	0
	初期位置 r	x 0, y 0
	初期速度 v	x 1, y 0
物体3	質量 m	1
	力 fx	vx[1]vx[2]-8/3vx[3]
	力 fy	0
	初期位置 r	x 0, y 0
	初期速度 v	x 1, y 0

計算時間をTmax=100として計算します。Time-vxのグラフを表示すると、$x,y,z$の時系列変化を見ることができます。

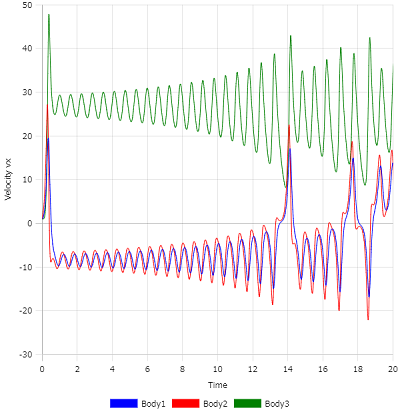
Time-vxグラフ（t=20までを表示）

$x$-$y$ や $x$-$z$ のプロットを表示したい場合は、ユーザー変数を使います。例えば、$x$-$z$ のプロットを作る場合は、ユーザー変数の物体１に次のように入力します。

物体1	px	vx[1]
物体1	py	vx[3]

px-pyのグラフを表示すると、$x$-$z$ のプロットになります。

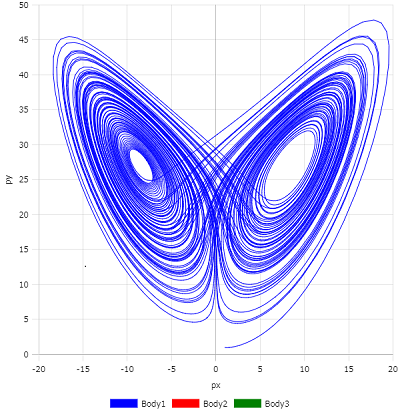
px-pyグラフ（$x$-$z$ に相当）

運動方程式

解く運動方程式は以下の形式のものです。

$$\frac{d x}{d t} = v$$

$$m \frac{d v}{d t} = F(t, x, v) $$

ここで、$t$：時間、$x$：位置、$v$：速度、$m$：質量、$F$：力

$x$は位置としていますが、変位や角度など何でも構いません。

数値計算法

4次のRunge-Kutta法

時間刻み固定で計算を行う場合は、４次のRunge-Kutta（ルンゲ=クッタ）法で計算を行います。

$$ \frac{dy}{dt} = f(t,y) $$

$$y_{n+1} = y_{n} + \frac{h}{6}(k_{1}+2 k_{2} + 2 k_{3} + k_{4})$$

$$t_{n+1} = t_{n} + h$$

$$k_{1} = f(t_{n},y_{n})$$

$$k_{2} = f(t_{n}+\frac{h}{2},y_{n}+\frac{h}{2} k_{1})$$

$$k_{3} = f(t_{n}+\frac{h}{2},y_{n}+\frac{h}{2} k_{2})$$

$$k_{4} = f(t_{n}+h,y_{n}+h k_{3})$$

Runge-Kutta-Fehlberg法

時間刻み自動制御で計算を行う場合は、Runge-Kutta-Fehlberg法が使われます。

$$ \frac{dy}{dt} = f(t,y) $$

$$k_{1} = f(t_{n},y_{n})$$

$$k_{2} = f(t_{n}+\frac{1}{4}h,y_{n}+\frac{1}{4}h k_{1})$$

$$k_{3} =f(t_{n}+\frac{3}{8}h,y_{n}+\frac{3}{32}h k_{1}+\frac{9}{32}h k_{2})$$

$$k_{4} = f(t_{n}+\frac{12}{13}h,y_{n}+\frac{1932}{2197}h k_{1}-\frac{7200}{2197}h k_{2}+\frac{7296}{2197} h k_{3})$$

$$k_{5} = f(t_{n}+h,y_{n}+\frac{439}{216}h k_{1}-8h k_{2}+\frac{3680}{513}h k_{3}-\frac{845}{4104}h k_{4})$$

$$k_{6} = f(t_{n}+\frac{1}{2}h,y_{n}-\frac{8}{27}h k_{1}+2h k_{2}-\frac{3544}{2565}h k_{3}+\frac{1859}{4104}h k_{4}-\frac{11}{40}h k_{5})$$

以上より、４次の解は、

$$y_{n+1} = y_{n} + h(\frac{25}{216} k_{1}+\frac{1408}{2565} k_{3} + \frac{2197}{4101} k_{4} - \frac{1}{5} k_{5}) $$

５次の解は、

$$z_{n+1} = y_{n} + h(\frac{16}{135} k_{1}+\frac{6656}{12825} k_{3} + \frac{28561}{56430} k_{4} - \frac{9}{50} k_{5} + \frac{2}{55} k_{6}) $$

となります。

ここで、５次の解と４次の解の差で誤差を評価します。

$$|z_{n+1}-y_{n+1}|=h \left| \frac{1}{360} k_{1}-\frac{128}{4275} k_{3} - \frac{2197}{75240} k_{4} + \frac{1}{50} k_{5} + \frac{2}{55} k_{6} \right| $$

許容誤差を$tol$とすると、

$$s = \left( \frac{tol \, h}{2 |z_{n+1}-y_{n+1}|} \right)^{1/5} $$

を係数として、時間刻みを$s \, h$として更新します。

$|z_{n+1}-y_{n+1}| \le tol \, h$であれば、誤差が許容範囲に収まったとして、４次の$y_{n+1}$を解として次の時間ステップに進み、誤差が大きい場合は新しい時間刻みで繰り返し計算します。

このように、４次と５次の誤差が大きいと時間刻みを自動的に小さく調整して行きます。例題の三体問題では物体どうしが接近した場合に力が大きくなるため、誤差が大きくなり時間刻みが小さくなります。