新型コロナウイルス(COVID-19)の感染拡大が世界中で大きな問題になっているが、こういった感染症を計算するための数理モデルがいくつかある。ここでは、SIRモデルとSEIRモデルと呼ばれる数理モデルを使って、感染症の時間推移を数値計算によってシミュレーションする。以下のフォームで、モデルのパラメータを変えて実際にシミュレーションを行うことができる。
目次
感染症の数理モデル
感染症を表現する数理モデルはいくつも提唱されているが、ここではSIRモデルとSEIRモデルを取り上げる。
SIRモデル
SIRモデル[1]は、集団を $S$(Susceptible、感受性者(非感染者))、$I$(Infectious、感染者)、$R$(Recovered、回復者(除去者))に分け、その間の遷移をモデル化したものである。図にすると下図のようになる。
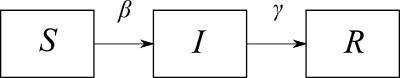
これは、化学反応と同様の反応式で表すと、
$$ S + I \xrightarrow{\beta} I $$
$$ I \xrightarrow{\gamma} R$$
となる。感染者 $I$ が 非感染者 $S$ と接触すると、速度定数 $\beta$ (感染率)で $I$ が増加し、$I$ は速度定数 $\gamma$ (回復率)で回復して $R$ となる。$R$ は免疫を獲得し、再び感染することはない($R$に死亡者を含めることもある)。
これを微分方程式で表すと、
$$ \frac{dS}{dt} = -\frac{\beta SI}{N}$$
$$ \frac{dI}{dt} = \frac{\beta SI}{N} - \gamma I$$
$$ \frac{dR}{dt} = \gamma I$$
となる。ここで、$N=S+I+R$ は集団の全人口。上式を足し合わせると右辺がゼロとなるため、$N$は一定で変化しないことがわかる。
SIRモデルは典型的な解として次のグラフ(横軸:日数、縦軸:人口)のようになる。$S$が減ると同時に、感染者 $I$ が増加する。$I$ はピークを迎え、やがて減少する。回復者 $R$ は増加していく。
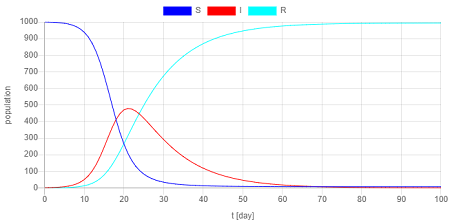
また、このモデルでは、$R_0=\beta / \gamma$ を基本再生産数(Basic reproduction number)と呼び、$R_0<1$ であれば流行が起こらない(下図)。感染率 $\beta$ が小さい場合などである。
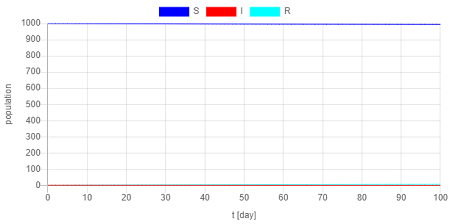
SEIRモデル
SIRモデルを発展させたモデルとして、SEIRモデルがある。これは、SIRモデルに $E$(Exposed、感染しているが感染性がなく潜伏期間中の者)を追加したモデルである。$S$ は $E$ を経て $I$ となる。このタイプのモデルは派生モデルとして多くのモデルが提唱されているが、ここでは人口増減やワクチン接種の効果を加味したSEIRモデル[2]を考える。

この集団では出生率 $\alpha$ で人口が増加し、死亡率 $\mu$ で人口が減少する。また、感染者 $I$ は感染症が原因で死亡率 $\delta$で減少する。また、$S$ はワクチンなどにより免疫を獲得し、$\nu$ の速度定数で $R$ となり感染を回避するという経路を持つ。なお、$\alpha = \mu = \delta = \nu = 0$であれば、最もシンプルなSEIRモデルとなる。
このモデルの方程式は、以下のようになる。
ここで、全人口 $N=S+E+I+R$ である。
人口増減がないシンプルなSEIRモデルでは次の図のような解となる。
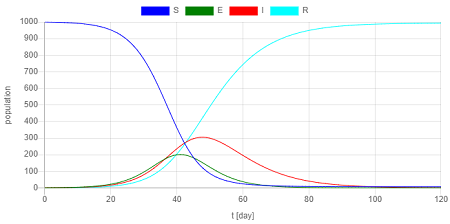
シミュレーション
ここでは、SIRモデルとSEIRモデルを数値的に解き、シミュレーションできる。モデルを選択し、各パラメータを入力して[計算実行]ボタンを押すと、結果のグラフが表示される。
入力値の説明
人口の単位は、[1人]。時間の単位は、[1日]としている。入力パラメータは次のとおり。
$S$:感受性者(非感染者)の初期値。単位[人]。
$E$:潜伏感染者の初期値。単位[人]。
$I$:感染者の初期値。単位[人]。
$R$:回復者の初期値。単位[人]。
$\alpha$:出生率。単位[1/日]。集団 $M$ 人が1日あたりに産む子供の数を $m$ 人とすると、$\alpha = m/M$。
$\mu$:自然死亡率。単位[1/日]。集団 $M$ 人での1日あたりの死亡者数を $m$ 人とすると、$\mu = m/M$。感染症を原因とする死亡者は含まない。
$\beta$:感染率。単位[1/日]。1人の人が1日あたり接触する人数を $m$ 人、感染者との接触により感染する確率を $p$ とすると、$\beta = m p$。
$\sigma$:発症率。単位[1/日]。感染症の潜伏期間を $D_E$ 日とすると、$\sigma = 1/D_E$。
$\gamma$:回復率。単位[1/日]。感染症の感染期間を $D_I$ 日とすると、$\gamma = 1/D_I$。
$\delta$:感染症を原因とする死亡率。単位[1/日]。感染者 $M$ 人での1日あたりの死亡者数を $m$ 人とすると、$\delta = m/M$。感染症以外が原因の死亡者は含まない。
$\nu$:回避率。単位[1/日]。集団内で1日あたり、ワクチン接種などにより感染を回避する人の割合。
$T$:計算期間。単位[日]。計算する日数。
数値解法
微分方程式の時間積分は、4次のRunge-Kutta法を用いた。時間刻みは $\Delta t = 0.01$ としている。
計算例
いくつかのパラメータで計算した例を示す。
モデルはSEIRモデルを使い、10000人の集団を考える。初期値として非感染者 $S$ =9990人、潜伏感染者 $E$ = 10人とする。出生や死亡は考えない。潜伏期間を5日として発症率 $\sigma$ = 1 / 5 = 0.2、感染期間を10日として回復率 $\gamma$ = 1 / 10 = 0.1 とした。また、$\alpha = \mu = \delta = \nu$ = 0 として計算する。
まず、感染率を1人が1日に10人と接触して、0.1の確率で感染するものとして $\beta$ = 10 * 0.1 = 1.0 で計算してみる。
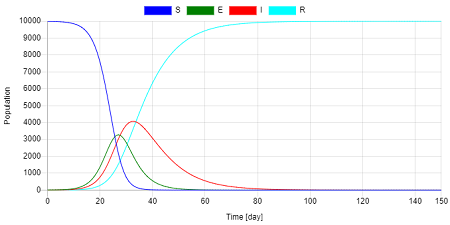
感染者 $I$ は急激に増加し、約30日で4000人に達してピークを迎えている。
次に、1日に接触する人数を7割削減し3人とすると $\beta$ = 0.3 となり、結果は下図のようになる。
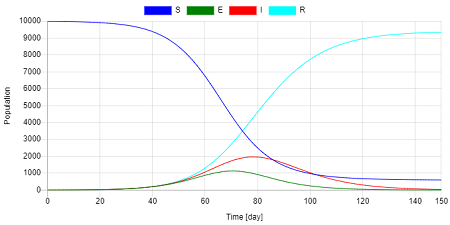
感染者 $I$ のピークが2000人程度に抑えられていることがわかる。また、感染者の増加が緩やかになっている。ただし、ピークの位置が後ろにずれるので、収束までに時間がかかる。外出制限などにより接触の機会を減らすことで、感染者のピークを減少させる効果はあると考えられる。
もし、ワクチン接種などで免疫を持ち感染しない人が増えるとどうなるか。1日に非感染者 $S$ の5%の人がワクチン接種するとして、回避率 $\nu$ = 0.05 で計算する。感染率は $\beta$ = 1.0。
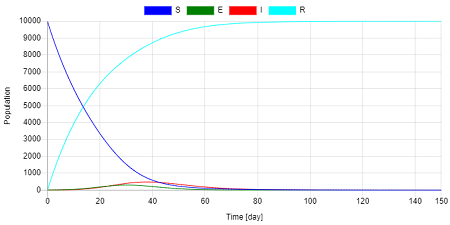
非感染者 $S$ が減り、ワクチン接種により免疫を獲得した回復者 $R$ が増加していく。感染者 $I$ のピークは大幅に減り500人弱となっている。
数値モデル自体は比較的簡単なものであるが、このようにパラメータを変更することで、机上で素早く効果を確認することができる。
注意事項
数理モデルはある仮定のもとに作られたものであり、数値計算の性格上、実現象を完全に再現するものではないことにご注意ください。
参考文献
[1] Kermack, W. O. ; McKendrick, A. G. A Contribution to the Mathematical Theory of Epidemics. Proc. Roy. Soc. of London. Series A, 1927, vol. 115, no. 772, p. 700-721.
[2] Biswas, M. H. A.; Paiva, L. T.; Pinho, M. D. A SEIR Model for Control of Infectious Diseases with Constraints. Mathematical Biosciences and Engineering, 2014, vol. 11, no. 4, p. 761-784.
