目次
BZ反応を計算する
ベロウソフ・ジャボチンスキー反応(Belousov-Zhabotinsky reaction、BZ反応)は、化学振動反応の一種で時間的、空間的に振動パターンを形成する面白い現象である。非平衡熱力学や非線形ダイナミクスの分野でも研究対象となっている。化学的には、硫酸水溶液中のセリウムなどの金属触媒によりマロン酸が臭素酸によって酸化される反応である。
筆者も昔、大学の化学実験でBZ反応をシャーレの中で再現し、美しい円形パターンを作ったのを覚えている。今回は、数値計算によりBZ反応の空間パターンをシミュレーションしてみる。
化学反応モデル
BZ反応のメカニズムはFKNメカニズムと呼ばれる複雑な反応メカニズム[1]が提唱されているが、ここではOregonatorと呼ばれるFKNメカニズムをより簡略化した反応モデルを使用する。Oregonatorは、オレゴン大学のFieldとNoyesにより考案されたモデル[2]で、5つの基本となる反応式で構成されている。
$$(\rm{R1}) \quad A+Y \xrightarrow{k_1} X + P$$
$$(\rm{R2}) \quad X+Y \xrightarrow{k_2} 2 P$$
$$(\rm{R3}) \quad A+X \xrightarrow{k_3} 2X+2Z$$
$$(\rm{R4}) \quad X+X \xrightarrow{k_4} A+P$$
$$(\rm{R5}) \quad B+Z \xrightarrow{k_c} \frac{1}{2}fY$$
ここで、$X(=\rm{HBrO_2})$、 $Y(=\rm{Br^-})$、 $Z(=\rm{Ce^{4+}})$ がモデルの変数で、$A(=\rm{BrO_3^-})$、 $B(=\rm{CH_2(COOH)_2})$ は一定とみなす。$P(=\rm{HOBr})$ は反応に直接寄与しないとする。
この反応モデルでは、(R1)で $Y$ から $X$ が生成され、(R3)で $X$ から $Z$、(R5)で $Z$ から $Y$ が生成されるという循環になっている。(R3)は自己触媒反応で、$X$ が自分の濃度を増加させる機構である。$Y$ の濃度が高くなると、(R2)の反応が促進され、$X$の自己触媒過程を抑制する。次に、$Y$ の濃度が低下すると、$X$ の自己触媒反応が促進し $Z$ が生成される。$Z$ が生成されると(R5)により再び $Y$ の濃度が高くなる。この循環を繰り返すことにより、振動反応が起こる。
この反応モデルの $X$、$Y$、$Z$ についての反応速度式は以下となる。
ここで、$x=2k_4X/(k_3A)$、$y=k2Y/(k_3A)$、$z=k_ck_4BZ/(k_3A)^2$、$\tau=k_cBt$、$\epsilon=k_cB/(k_3A)$、$\epsilon'=2k_ck_4B/(k_2k_3A)$、$q=2k_1k_4/(k_2k_3)$ と置くと、
$$\epsilon \frac{dx}{d\tau} = qy-xy+x(1-x)$$
$$\epsilon' \frac{dy}{d\tau} = -qy-xy+fz$$
$$\frac{dz}{d\tau} = x-z$$
という、Tysonの式となる[3]。さらに、$\epsilon' \ll \epsilon$ とすると、$y=fz/(x+q)$と近似され、次の簡略化された2変数の方程式となる。
$$\epsilon \frac{dx}{d\tau} = x(1-x)-fz \frac{x-q}{x+q}$$
$$\frac{dz}{d\tau} = x-z$$
BZ反応による空間パターンを計算するため、上式に拡散項を付加する。
$D_x$、$D_z$ はそれぞれ $x$、$z$ の拡散係数である。この式は反応拡散方程式とよばれ、今回の計算にはこの式を用いる。
計算手法
BZ反応はセルオートマトンにより計算されている例があるが、今回のシミュレーションでは空間方向の伝播は差分法により解き、上式をそのまま数値的に解くことにする。空間は2次元平面として、拡散項は2階中心差分とし、時間積分は1次のオイラー法を用いた。長さ2✕2の空間を200✕200の格子に分割し、境界条件は周期境界条件とした。
各パラメータは以下のとおりである。
$f=0.95$、$\epsilon=0.08$、$q=0.0075$、時間刻み$\Delta \tau=0.001$
計算結果
BZ反応は、時間的に振動する反応が空間的に広がり、円形パターン(target pattern)やスパイラルパターン(spiral pattern、螺旋)などを形成することが知られている。
時間振動
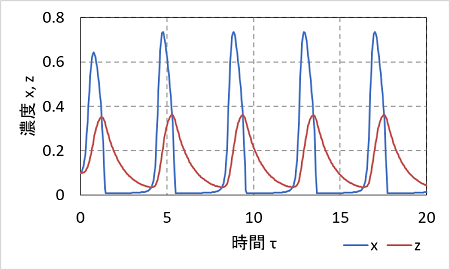
まず、空間パターンの計算の前に、0次元で拡散が無い状態で時間振動の様子を見る。グラフは、$x$ と $z$ の濃度の時間変化である。初期は $x=y=0.1$ とした。$x$ がピークとなったあとやや遅れて $z$ がピークとなり規則正しく振動を繰り返している。
次に、2次元の計算結果を動画で示す。
円形パターン
初期条件は、平衡点濃度 $(x_0,z_0)$ で一様とした空間に、適当な箇所にその濃度の1.01倍となる点をおいた。拡散係数は、$D_x=D_z=1.0 \times 10^{-5}$ とした。
動画は $z$ の濃度コンター図である。BZ反応の実験でよくみる結果と同様に、同心円の波形が広がっていき、隣の円形パターンと干渉していく様子がわかる。
※平衡点:方程式の平衡点(安定な濃度)は、式の左辺の微分項をゼロとして、$x$ と $z$ について解くと求まる。この方程式では、以下が平衡点の濃度である。
スパイラル(螺旋)パターン
初期条件は、方程式の平衡点 $(x_0,z_0)$ を与え、1%のランダムな撹乱を加えた。拡散係数は、$D_x=5.0 \times 10^{-4}$、$D_z=5.0 \times 10^{-6}$ とした。
初期にはランダムであった場が自己組織化し、くるくるカールする螺旋パターンを形成していく様子がわかる。実際のBZ反応では、円形パターンに対して円の一部を引っ掻いて撹乱を加えてやると、螺旋パターンが形成される。
他にもパラメータによって様々なパターンが形成されるので、この方程式系は興味深い。
参考文献
[1] Field, R. J.; Korös, E.; Noyes, R. M. Oscillations in Chemical Systems II. Thorough analysis of temporal oscillations in the bromate-cerium-malonic acid system. J. Am. Chem. Soc. 1972, vol. 94, no. 25, p. 8649-8664.
[2] Field, R. J. ; Noyes, R. M. Oscillations in Chemical Systems IV. Limit cycle behavior in a model of a real chemical reaction. J. Chem. Phys. 1974, vol. 60, p. 1877-1884.
[3] Tyson, J. J. A quantitative account of oscillations, bistability, and traveling waves in the Belousov-Zhabotinsky reaction. Oscillations and Traveling Waves in Chemical systems. Field, R. J.; Burger, M. Eds., New York, John Wiley & Sons, 1985.
