これまで、データ構造としてリスト構造についてお話しました。
今回は木構造というデータ構造について解説したいと思います。
目次
木構造とは
木(ツリー)構造とは下図のような木のような形をしたデータ構造です。
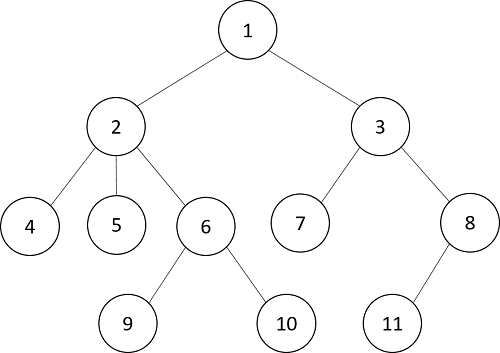
この図では、1番の丸を起点として2つに枝分かれしています。2番の丸は3つの枝に分かれています。6番はさらに2つに枝分かれしていることがわかります。
木が伸びて枝分かれしていく様子と似ていることから木構造と呼ばれています。実際の木は上に向かって伸び枝分かれしていきますが、データの木構造は上下逆さまにして下に向かって枝が伸びていくように描かれます。
我々の身の回りでも木構造はよく見かけます。例えば、会社などの組織図で部の下に課が分かれていたり、その下にさらにチームが分かれていたりするものは、木構造の形で描かれます。また、家系図など親と子の関係を表すような系図も木構造を用いて表記されています。
木構造において、各丸はノード(node)とか節と呼ばれ、データとして何かの値を持っています。下の図では、ノードは数値データを持っています。
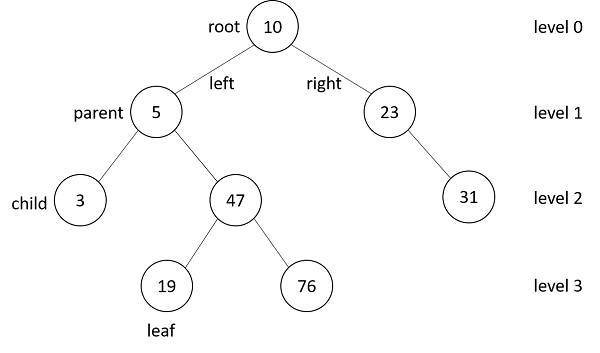
ツリーの一番上のノードを根(root)と呼び、構造の起点となります。ノードが枝分かれすると、そのノードは親(parent)となり、その下のノードは子(child)ノードとなります。木の末端のノードは葉(leaf)と呼ばれ、そのノードからは枝が伸びていません。また、木構造の深さはレベル(level)で表し、rootノードをレベル0として、レベル1、2という具合に深くなっていきます。
この図を見ると、ノードから伸びる枝は最大2つです。このような木を二分木と呼びます。もちろん、枝が4つまで分かれることが出来る四分木のような多分木を定義することもできます。今回は二分木を考えていきましょう。
二分木はノードから左(left)、右(right)の2方向に枝分かれしていきます。枝は2つに分かれる場合もあれば、左か右のどちらか一方にだけ伸びる場合もあります。
この木をデータ構造として見ると、以前学んだリスト構造と同様に考えることができます。各ノードは子ノードに連結しているため、ノードを子ノードへの連結器を含めて表現することができます。上図をデータの連結の形で図示すると
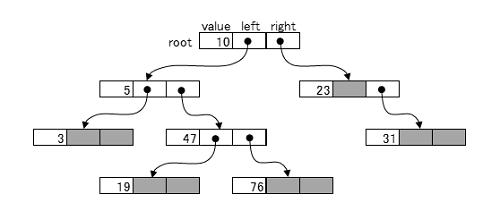
と表すことができます。この図を見るとリスト構造のときと同じように、leftとrightに次のノードを連結していくだけで、プログラムが書けることがわかります。
二分探索木
複数のデータの中からあるデータを見つけることを探索と言いますが、この探索を効率的に行うのに木構造が使われます。探索に使われる木構造は探索木と呼ばれます。データベースの探索などでは、実際に探索木が使われていますが、ここでは探索木の中でも最も基本的な二分探索木を見ていきましょう。
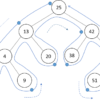
二分探索木はデータを二分木の構造で持たせています。数値データで考えると、以下のような二分木になります。
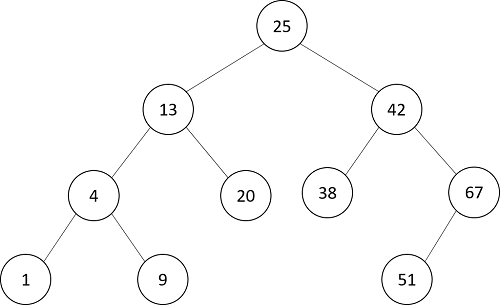
まず、ルートの値を25とすると、左側にそれより小さな数値13が置かれています。そして右側には25より大きな42が格納されています。つまり以下同様に、
「親ノードの値より小さなデータは左の子ノードに、大きなデータは右の子ノードに配置する。」
というルールによって作られていることがわかります。どのノードを見てもそうなっています。例えば、42より小さな38は左に、大きな67は右にあります。このルールに基づいて作られている二分木が二分探索木になります。
この二分探索木を使うとデータを簡単に見つけることが出来ます。例えば20を探すには、ルートの25と比較して小さいので左の枝をたどる、次に13と比べて大きいので右の枝をたどる。すると20が見つかる。つまり、25→13→20とノードを3つたどるだけで、見つけることができました。
このように、「目的の値をノードの値と比較して、小さければ左の枝を、大きれば右の枝をたどるという操作を値が一致するまで繰り返す」ことによって探索することができます。
ばらばらのデータの中からデータを探索する方法は色々ありますが、探索木を使う方法も効率的な方法としてよく採用されています。
二分探索木のプログラム
では、二分探索木をPythonでプログラミングしてみましょう。プログラムとしては、リストと同様にノードを表すクラスと二分探索木のクラスを作り、そのメソッドを実装していきます。ここでは、ツリーにデータを挿入するメソッドと、データを探索するメソッドを作ることにしましょう。
ノードのクラス
まず、ツリーのノードを表すクラスTreeNodeを定義します。
class TreeNode:
def __init__(self, value = None):
self.value = value
self.left = None
self.right = Noneプロパティは、値(value)、左の子ノード(left)、右の子ノード(right)を持たせます。ノードを定義した時点では、子ノードはNoneとしておきます。
二分探索木のクラス
次に二分探索木を表すクラスBinarySearchTreeを作ります。
class BinarySearchTree:
def __init__(self):
self.root = Noneルートノードを表すrootをプロパティに持たせます。最初は空でNoneにしておきます。
データを挿入するメソッド
ツリーにデータを挿入するメソッドinsertを定義します。
def insert(self, value):
if self.root == None:
self.root = TreeNode(value)
return
node = self.root
while True:
if value < node.value:
if node.left == None:
node.left = TreeNode(value)
return
node = node.left
else:
if node.right == None:
node.right = TreeNode(value)
return
node = node.rightまず最初のif文は、rootが空のときにrootにノードを挿入するためのものです。
rootが存在する場合は、はじめにnodeをrootとして、ルートから木をたどります。while Trueはずっと繰り返すための命令です。if文で引数valueがnodeの値より小さければnode.leftをたどります。このとき、node.leftがNoneつまり左の子ノードが空であれば、そこに新しくノードを定義してreturnで抜けます。
同様にvalueがnode.valueより大きければ、右のnode.rightをたどり空であれば挿入します。
データを探索するメソッド
最後にデータを探索するメソッドsearchを定義しておきます。
def search(self, value):
node = self.root
while node != None:
print(node.value, end=" ")
if value == node.value:
print()
return node
elif value < node.value:
node = node.left
else:
node = node.right
return None 引数はvalueとし、この値のノードを見つけて返します。
まず、nodeをrootにして、while文でnodeがNoneになるまでたどります。ここでは、たどった道筋がわかるようにノードの値をprintしています。
次のif文では、valueがnodeの値と同じであれば見つかったので、そのときのnodeを返します。もしvalueがnodeの値より小さければ左のnode.leftをたどり、大きければ右のnode.rightをたどります。もし最後までたどっても見つからなければNoneを返すようにしています。
ツリーの作成と探索の実行
これで、二分探索木のクラスができたので、実際にツリーを作成し探索を実行してみたいと思います。
tree = BinarySearchTree()
tree.insert(25)
tree.insert(13)
tree.insert(20)
tree.insert(42)
tree.insert(67)
tree.insert(4)
tree.insert(51)
tree.insert(38)
tree.insert(1)
tree.insert(9)
node = tree.search(20)
print(node.value)まずtree変数に二分探索木のオブジェクトを定義します。次にinsertメソッドでデータを挿入していきます。ここではこの順番で挿入すると、下図のツリーが出来上がります。

node = tree.search(20)は20の値を持つノードを探索して、変数nodeに代入しています。最後に、print(node.value)でその値を出力しています。
これを実行すると、25 13 20と木をたどった道筋が出力されるので、どのように探索されたかがわかります。
全体のプログラム
今回作ったプログラム全体を載せておきます。
class TreeNode:
def __init__(self, value = None):
self.value = value
self.left = None
self.right = None
class BinarySearchTree:
def __init__(self):
self.root = None
def insert(self, value):
if self.root == None:
self.root = TreeNode(value)
return
node = self.root
while True:
if value < node.value:
if node.left == None:
node.left = TreeNode(value)
return
node = node.left
else:
if node.right == None:
node.right = TreeNode(value)
return
node = node.right
def search(self, value):
node = self.root
while node != None:
print(node.value, end=" ")
if value == node.value:
print()
return node
elif value < node.value:
node = node.left
else:
node = node.right
return None
tree = BinarySearchTree()
tree.insert(25)
tree.insert(13)
tree.insert(20)
tree.insert(42)
tree.insert(67)
tree.insert(4)
tree.insert(51)
tree.insert(38)
tree.insert(1)
tree.insert(9)
node = tree.search(20)
print(node.value)まとめ
今回は木構造と二分探索木について説明しました。次回はもう少し二分探索木の特徴についてお話しておきたいと思います。