今回は数値計算のプログラムでよく使われるソート(並べ替え)について解説します。
目次
ソートとは
配列などのデータがあった場合、要素の小さい(または、大きい)値から順番に並べ替える処理はよく出てきます。これをソート(sort)と言います。
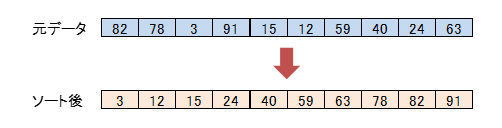
ソートには、さまざまな種類のアルゴリズムが考えられています。各プログラミング言語には既にライブラリなどでソートが使えるものが多くあります。それらを使えば自分でプログラミングする手間は省けますが、内部の処理がどのようなアルゴリズムで行われているのかを知っておくことは数値計算をする上で有益かと思います。
ここでは、いくつかのソートのアルゴリズムをご紹介します。プログラム言語にはPythonを使います。
※もちろんPythonでもソートをはじめ様々な処理がブラックボックスで使えますが、ここではあえて冗長に書いて理解を深めることにします。
選択ソート
ある配列データを要素の値の小さい順に並べ替えるプログラムを考えます。一番オーソドックスな方法は、全ての要素から一番小さな要素を見つけ先頭の要素と入れ替える方法です。さらに先頭以外の要素の中から一番小さな要素を見つけ先頭の次の要素と入れ替えます。これを順々に行って、並べ替えていくというものです。
つまり、配列a(要素数n)を小さい順にソートするアルゴリズムは、
①まず、a[0]からa[n-1]の中から最小の要素を見つけ、a[0]と入れ替える。
②次に、a[1]からa[n-1]の中から最小の要素を見つけ、a[1]と入れ替える。
③以降、同様にn-1回繰り返す。
と書けます。この方法は選択ソートと呼ばれています。
これをPythonプログラムにした例を以下にあげます。
def swap(a, i, j):
tmp = a[i]
a[i] = a[j]
a[j] = tmp
def selection_sort(a):
n = len(a)
for i in range(n-1):
min = a[i]
pos = i
for j in range(i+1, n):
if a[j] < min:
min = a[j]
pos = j
swap(a, i, pos)
a = [82, 78, 3, 91, 15, 12, 59, 40, 24, 63]
print(a)
selection_sort(a)
print(a)
swap関数は配列aのiとjの要素を入れ替える関数です。selection_sortが選択ソートのメイン関数です。二重のforループになっていて、外側は、n-1回繰り返され、それぞれに対して内側のループで最小値を探してその要素を探索の先頭の要素と入れ替えています。
10個の要素を持つ配列a = [82, 78, 3, 91, 15, 12, 59, 40, 24, 63]を使ってソートの様子を見てみます。
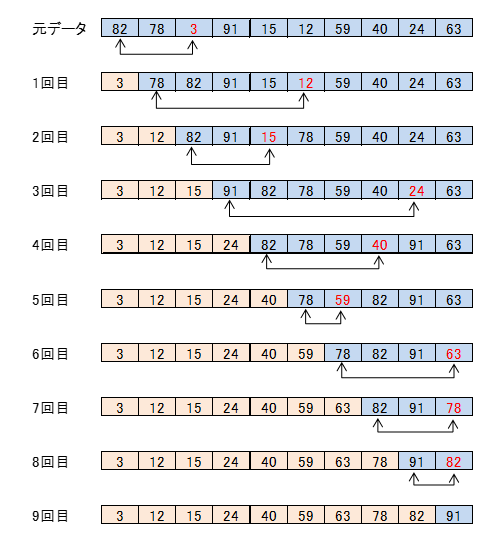
選択ソート
最初全てのデータの中から最小値3を見つけ先頭の要素82と入れ替えます(1回目)。次に1回目の青色領域で最小値12を見つけ、その先頭の78と入れ替えます(2回目)。これを順に9回繰り返すと小さい順にソートされた配列が出来上がります。
バブルソート
選択ソートと似たようなソート方法にバブル(bubble)ソートと呼ばれるアルゴリズムがあります。これは次のようなものです。
①まず、最後のa[n-1]要素から先頭のa[0]に向けて逆順に②の操作をしていく。
②隣り合う要素の大きさが逆転していたら、その2つの要素を入れ替える。
③先頭まで操作すると、先頭に最小の値が現れる。
④これを同様にn-1回繰り返す。
バブルソートのプログラム例を以下にあげます。
def swap(a, i, j):
tmp = a[i]
a[i] = a[j]
a[j] = tmp
def bubble_sort(a):
n = len(a)
for i in range(n-1):
for j in range(n-1, i, -1):
if a[j-1] > a[j]:
swap(a, j-1, j)
a = [82, 78, 3, 91, 15, 12, 59, 40, 24, 63]
print(a)
bubble_sort(a)
print(a)これも二重のループになっており、外側はn-1回繰り返され、内側はn-1からi+1まで逆順に繰り返されます。隣り合うa[j-1]がa[j]より大きいと入れ替えています。
この並び替えの様子を図示すると、

バブルソート
となっています。回を追うごとに順に小さな要素が操作領域の先頭まで浮かび上がってきます。ちょうど泡が水面に浮かび上がってくるイメージなので、バブルソートと呼ばれています。
ソートの計算量
選択ソートとバブルソートは、どちらも二重のループになっていて、外側はn-1回、内側のループは平均でn/2回まわります。つまり、並べ替えにかかる計算量はnの2乗オーダー$o(n^2)$であることがわかります。要素数が少ないうちはよいですが、要素が多くなるとかなり計算量が多くなります。
これらのソートはアルゴリズムは簡単でプログラミングも楽ですが、計算時間がボトルネックとなります。そこで、実用的には以下のような別のソートアルゴリズムが考えられています。

