今回は数値計算のプログラムでよく使われる再帰関数について解説します。
再帰関数とは
再帰関数(Recursive Function)とは関数の中で自分自身の関数を呼び出している関数のことです。
例えば$n$の階乗$n!$を求める関数を作りましょう。プログラミング言語はPythonです。
普通はfor文を使って、
def factorial(n):
f = 1
for i in range(2, n+1):
f *= i
return f
a = factorial(5)
print(a) のように関数factorialを作ることが考えられます。forループで単純に1からnまで掛け合わせるという単純なものです。
これは再帰関数を使うと
def factorial(n):
if n == 0:
return 1
return n * factorial(n-1)
a = factorial(5)
print(a) のように書くことができます。factorial関数の中でfactorial関数が呼ばれています。この関数がやっていることは、引数nが0のときには1を返し、それ以外ではn*factorial(n-1)を返しています。
この関数呼び出しのイメージは以下のようになっています。
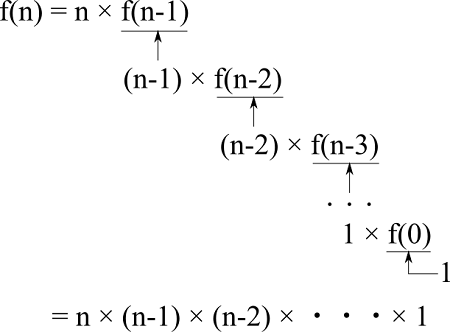
関数の引数はn-1と1ずつ減っていき、最終的に0になるまで繰り返されます。
このように再帰関数を使うとプログラムを簡潔に書くことができます。この例だとfor文を使って書いてもさほど不便を感じないかも知れませんが、ループさせる回数が不明だったり、ループが何重にも重なっているような場合などは再帰関数の方がシンプルに書けます。
最大公約数を求める
具体的な例をあげてみましょう。ある2つの自然数a、bがあったときにその最大公約数を求める関数を作ります。
最大公約数を求めるアルゴリズムに、ユークリッドの互除法というのがあります。ユークリッドの互除法は
2つの自然数a、b(a≧b)があったとき、aをbで割ったあまりをrとすると、aとbの最大公約数とbとrの最大公約数は等しい
という性質によって、最大公約数を求めるものです。
例えば、a=2752、b=1936とすると、
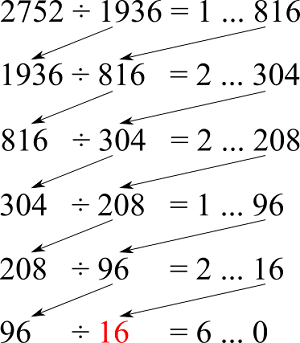
のように、割る数を余りで順次割っていき、余りが0になったときの、割る数が最大公約数として求まります。上の性質によれば、最初の2752、1936の最大公約数と最後の96、16の最大公約数は等しいので、16が最大公約数だということがわかります。
このアルゴリズムを再帰関数を使って書くと、
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)となります。a%bはaをbで割った余りを計算するものです。関数では最終的に引数b(余りに相当)が0になったらaをそのまま返しているので、その時点まで再帰的に繰り返されます。
これもfor文などの繰り返し処理を使って書けなくはないですが、再帰関数を使うととてもシンプルに書くことができます。
これを使った最大公約数と最小公倍数を求めるプログラムをあげておきます。
def gcd(a, b):
if b == 0:
return a
return gcd(b, a % b)
def lcm(a, b):
return a * b // gcd(a, b)
a = 2752
b = 1936
g = gcd(a, b)
l = lcm(a, b)
print("GCD = ", g)
print("LCM = ", l) lcmは最小公倍数を求める関数で、aとbの積をその最大公約数で割ったものが最小公倍数になります。(//はPythonでは整数除算になります。)
再帰関数の注意
再帰関数はプログラムをシンプルにできてよいのですが、再帰関数の呼び出しが何重にもなる(深くなる)とエラーが出る場合があります。プログラミング言語や環境によって制限が決まっていますが、Pythonの筆者の環境では1000回程度を超えるとエラーで停止します。
import sys
print(sys.getrecursionlimit())で再帰の制限回数を出力することができます。また、
sys.setrecursionlimit(5000)で制限回数を増やすことも可能です。ただし、使用している環境によりどこまで大きくできるかは変わってきます。いずれにしても、再帰の深さがどの程度になるかは予め把握した上でプログラミングする必要があります。
