【科学技術計算講座5-7】SPH法の密度、圧力

前回はSPH法の離散化についてお話しました。

今回はSPH法の密度、圧力の計算方法について説明します。

粒子クラス

物性値について説明する前に、プログラム上の粒子の扱い方について決めておきたいと思います。以前少しお話したように、流体粒子は複数個ありますが、その一つ一つの粒子はオブジェクトとして定義することにします。そこで、元となる粒子クラスを作っておきます。

class Particle {
  constructor(x = 0, y = 0) {
    this.position = new Vector(x, y);
    this.velocity = new Vector();
    this.velocity2 = new Vector();
    this.force = new Vector();
    this.pressure = 0;
    this.density = 0;
    this.active = true;
  }
}

クラス名はParticleとしましょう。コンストラクターは初期座標x、yを引数として、以下のプロパティを持たせます。

position：位置ベクトル、velocity：速度ベクトル、velocity2：速度ベクトル、force：力ベクトル、pressure：圧力、density：密度、active：計算領域内に存在するかどうかのフラグ

各プロパティの詳細は追々説明していきます。粒子クラスにはメソッドもいくつか持たせますが、これもその都度付け加えていきます。ここでは、ひとまず粒子クラスを作って、粒子をオブジェクトで定義するということだけ承知しておいてください。

プログラム上は粒子を１個作るには、

let p = new Particle(x, y);

のようにすれば、変数pに初期位置(x,y)の粒子オブジェクトを定義できます。

粒子は１個だけでなく数多く定義する必要があるので、pを配列にしてその配列要素が１個の粒子オブジェクトを表すことにしましょう。例えば、矩形の領域に粒子を並べながらオブジェクト定義していくJavaScriptプログラムの例は、

let p = [];
for (let i = 0; i < nx; i++) {
  for (let j = 0; j < ny; j++) {
    const x = (i + 0.5) * particleSize;
    const y = (j + 0.5) * particleSize;
    p.push(new Particle(x, y));
  }
}

のように書くことができます。particleSizeという間隔で粒子を配置しています。

密度の定式化

では流体の密度はどのように計算すればよいでしょうか。物理量は前回離散化したとおり次式で表すことができます。

$$\phi({\bf r}_i) = \sum_j \frac{m_j}{\rho_j} \phi({\bf r}_j) W({\bf r}_i-{\bf r}_j) \tag{7-1}$$

ここでは密度を表すので、

$$\begin{split} \rho({\bf r}_i) &= \sum_j \frac{m_j}{\rho_j} \rho({\bf r}_j) W({\bf r}_i-{\bf r}_j) \\ &= \sum_j m_j W({\bf r}_i-{\bf r}_j) \end{split} \tag{7-2}$$

となります。流体の密度場は(7-2)式の分布を持つということになります。

ここで、一つ疑問が起こります。【5-5】章で議論したように、非圧縮性を考えた場合、流体の密度は一定です。しかし、(7-2)式の分布を持つということは、完全には非圧縮性を満たしていないことになります。つまりここでは、圧縮性を考慮した擬似的な非圧縮性のモデル化を行っていくことになります。

圧力の式

一方、圧力はナビエ＝ストークス方程式の右辺に出てきます。

$$\frac{D {\bf v}}{D t} = -\frac{1}{\rho} \nabla p + \frac{\mu}{\rho} \nabla^2 {\bf v} + {\bf g} \tag{7-3}$$

ところが、連続の式にもナビエ＝ストークス方程式にも圧力自体を表す式は出てきません。格子法などで使われる完全な非圧縮性の解析手法であれば、連続の式から導かれる次式

$$\nabla \cdot {\bf v} = 0 \tag{7-4}$$

を速度場が満たすように圧力を決めてやります。

しかしここでは、（7-4)式は使わない（つまり、連続の式は使わない）ことにします。どうするかというと、密度と圧力を結びつける状態方程式を導入して、圧力を密度場から決めることにします。状態方程式は、皆さんご存知の理想気体の状態方程式などがあります。SPH法でもいくつか状態方程式が提唱されていますが、ここでは「圧力は基準密度からの差に比例する」と仮定して次式で定義します[1]。

$$p = k (\rho - \rho_0) \tag{7-5}$$

$\rho_0$は基準密度、$k$は剛性を表す係数です。この式は、基準密度より密度が大きくなると圧力が大きくなることを意味しています。密度と圧力、流れの関係は以下のようなイメージになります。

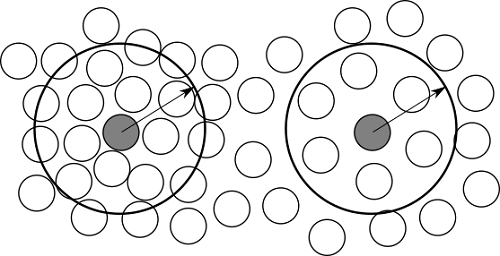
（左）密度・圧力＝大、（右）密度・圧力＝小

①もし流体粒子が密集していると、(7-2)式により局所的に密度が大きくなります。
②すると(7-5)式によりその場の圧力が大きくなります。
③流体粒子はナビエ＝ストークス方程式より、圧力が大きいところから小さい方へ向かって力が働き、結果として密集状態を解消して基準密度になろうとします。
④最終的に均一な密度になり非圧縮性が保たれる方向に向かうというわけです（※）。

※実際には、重力などの外力があると、外力と圧力勾配が釣り合う状態になります。

プログラム

では、密度と圧力を計算するためのJavaScriptプログラムを作っておきましょう。

function densityPressure() {
  const calcDP = function(p) {
    for (let i = 0, n = p.length; i < n; i++) {
      if (!p[i].active) continue;
  
      let density = 0;
      p[i].forNeighbor(cell, function(pNeighbor, rv) {
        const r = rv.magnitude();
        density += w.kernel(r) * massParticle;
      });
      p[i].density = density;
      p[i].pressure = Math.max(stiffness * (p[i].density - density0), 0);
    }
  };

  calcDP(p);
  calcDP(pWall);
}

密度、圧力の計算はdensityPressure()という関数にします。

const calcDP = function(p) {...};

の部分は、calcDPという関数を定義しています。JavaScriptでは関数の中にも関数を定義することができます。calcDP関数で具体的に密度と圧力を計算しています。引数のpは粒子オブジェクトを格納した配列です（上述）。

for (let i = 0, n = p.length; i < n; i++) {

このfor文は、粒子配列pをすべての粒子に対して回しています。つまり、すべての粒子に対して、密度・圧力を計算しています。

if (!p[i].active) continue;

p[i].activeは、前述の粒子オブジェクトのプロパティを表します。activeプロパティは別の箇所で、「その粒子が計算領域内にあれば true、領域から出ると false 」に設定されます。つまり、領域から出た粒子を計算対象から除外するためのフラグになります。continue文は、JavaScriptでは「これ以下を処理しないで、次のforループに移る」という命令です。要するに、「p[i].activeがfalseなら密度・圧力は計算しない」ということになります。

let density = 0;
p[i].forNeighbor(cell, function(pNeighbor, rv) {
  const r = rv.magnitude();
  density += w.kernel(r) * massParticle;
});
p[i].density = density;

ここは密度を計算する部分です。p[i].forNeighborは「粒子iの近傍の粒子に対してループする」という粒子オブジェクトのメソッドです。これについては、別の章で詳しく説明するので、ここでは近傍粒子に対するループということだけ認識しておいてください。rvは粒子iと近傍粒子の間の距離ベクトルです。密度の計算は(7-2)式のとおりで、カーネル関数に粒子質量massParticelを掛けて、近傍粒子に対して足し合わせています。p[i].densityは、粒子オブジェクトのdensityプロパティで、密度を格納しています。

p[i].pressure = Math.max(stiffness * (p[i].density - density0), 0);

最後に、計算した密度をもとに(7-5)式で圧力を計算して、プロパティに格納しています。ここで、Math.maxは引数のうちの最大値を返すという数学関数です。つまり、圧力が負にならないように制御しています。(7-5)式だと密度が基準密度より小さくなると圧力が負になりますが、密集度が小さい場合に過大な引力が発生してしまうのを避けるためのものです。

  calcDP(p);
  calcDP(pWall);

ここは、定義したcalcDP関数を実行する部分です。pは流体粒子オブジェクトの配列、pWallは壁面粒子オブジェクトの配列で、それぞれ密度・圧力を求めています。

まとめ

SPH法の密度と圧力についてお話しました。また、JavaScriptで密度・圧力を計算するプログラムを作成しました。

次回は近傍粒子の探索方法について説明したいと思います。

参考文献

[1] Müller, M.; Charypar, D.; Gross, M. Particle-Based Fluid Simulation for Interactive Applications. In Proc. of the 2003 ACM SIGGRAPH/Eurographics Symposium on Computer
Animation. 2003, p. 154–159.

←前回　SPH法の離散化
 →次回　近傍粒子の探索

全体の目次