前回はJavaScriptのオブジェクト指向プログラミングについて少しふれました。
今回からSPH法に入っていきます。まず初めにSPH法の基本となる流体の基礎方程式であるナビエ=ストークス方程式と連続の式について説明しておきたいと思います。
目次
流体の基礎方程式
本講座で取り扱うSPH法では流体の計算を行います。ここで扱う流体の基礎方程式は、次に示す連続の式とナビエ=ストークス方程式(Navier-Stokes equation)です。
連続の式
$$\frac{D \rho}{D t} + \rho \nabla \cdot {\bf v} = 0 \tag{5-1}$$
ナビエ=ストークス方程式
$$\frac{D {\bf v}}{D t} = -\frac{1}{\rho} \nabla p + \frac{\mu}{\rho} \nabla^2 {\bf v} + {\bf g} \tag{5-2}$$
ここで、$\rho$:密度、${\bf v}$:速度ベクトル、$p$:圧力、$\mu$:粘性係数、${\bf g}$:重力加速度ベクトル。
また、$D/Dt$というのは流体とともに移動する流体粒子で見たときの時間変化率を表します(詳細は後で説明します)。
以下では、これらの式について導出を含めて簡単に説明します。
連続の式
連続の式は、いわゆる質量保存を表す式です。今、流体とともに移動する微小体積の流体粒子を考えます。この粒子の体積を$\Delta V = \Delta x \Delta y$とします。ここでは簡単のために2次元で考えましょう。
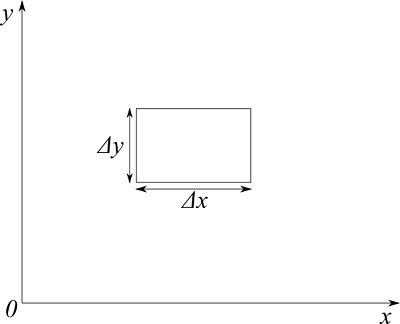
密度を$\rho$とすると、質量は$\rho \Delta V$です。質量の生成消滅がなく保存されるとすると、
$$\frac{D (\rho \Delta V)}{D t} = 0 \tag{5-3}$$
と表すことができます。質量の時間変化が無いということです。この式を変形すると、
$$\frac{D \rho}{D t} \Delta V + \rho \frac{D \Delta V}{D t} = 0 \tag{5-4}$$
となります(高校で習う積の微分です)。さらに左辺第二項を、
$$\begin{split} \frac{D \Delta V}{D t} &= \frac{D \Delta x \Delta y}{D t} \\ &= \frac{D \Delta x}{D t} \Delta y + \Delta x \frac{D \Delta y}{D t} \\ &= \Delta v_x \Delta y + \Delta x \Delta v_y \end{split} \tag{5-5}$$
を用いて変形すると、
$$\frac{D \rho}{D t} + \rho (\frac{\Delta v_x}{ \Delta x} + \frac{\Delta v_y}{ \Delta y} ) = 0 \tag{5-6}$$
となります($v_x$、$v_y$は速度のx、y成分)。ここで、$\Delta x \rightarrow 0$、$\Delta y \rightarrow 0$の極限を取ると、
$$\frac{D \rho}{D t} + \rho (\frac{\partial v_x}{ \partial x} + \frac{\partial v_y}{ \partial y} ) = 0 \tag{5-7}$$
となり、(5-1)式となります。
さてここで、密度が一定で変化しない非圧縮性流体を考えます。すると(5-1)式の左辺第一項はゼロとなるので、
$$ \nabla \cdot {\bf v} = 0 \tag{5-8}$$
が成り立ちます。これは以前、有限体積法のところで説明したとおり、湧き出しも吸い込みもない状態を表しています。
ナビエ=ストークス方程式
ナビエ=ストークス方程式は流体の運動方程式を表す式です。運動方程式は御存知の通り、$m$を質量、$a$を加速度、$F$を力とすると、
$$m a = F \tag{5-9}$$
という形をしています。流体に働く力が分かれば、運動方程式をたてることができます。
では、まず左辺から見ていきましょう。先ほどと同様に、微小体積領域を考えます。質量は$\rho \Delta x \Delta y$、加速度は$D {\bf v}/ D t$なので、(5-9)式の左辺は、
$$m a = \rho \Delta x \Delta y \frac{D {\bf v}}{ D t} \tag{5-10}$$
と表せます。
次に、右辺の力を考えます。
外力項
一番最初に簡単な形の外力項を考えます。質量を持つ物体には重力が働きます。流体にも重力が働いています。微小領域に働く重力${\bf F}$は、重力加速度ベクトルを${\bf g}$とすると、質量×加速度なので、
$${\bf F} = \rho \Delta x \Delta y {\bf g} \tag{5-11}$$
と表せます。
圧力項
次に圧力を考えましょう。流体は圧力の高いところから低いところに流れるというのはイメージできると思います。気象の高気圧・低気圧とか、高圧の風船から勢いよく空気が出ていくとか、流体は圧力によって運動しています。圧力はある面に対して垂直方向に働く力です。
今、微小流体領域のx方向を考えたとき、左側の面の圧力を$p$とすると、右側の面には $p + (\partial p / \partial x) \Delta x$の圧力が働いています(x方向の勾配分だけ増加している)。
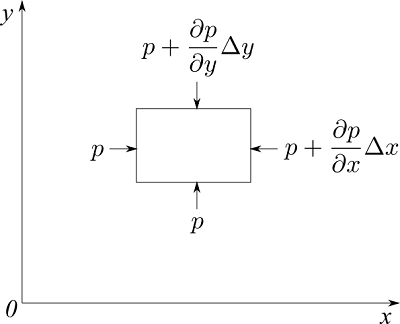
したがって、微小領域のx方向に働く正味の力は、
となります。圧力$p$は単位面積あたりの力なので、x方向の面の面積$\Delta y$をかけると力になります。同様に、y方向にも
の力が働きます。つまり、圧力による力は、
$${\bf F} = - \nabla p \Delta x \Delta y \tag{5-14}$$
となります。
粘性項
次に粘性力を考えます。ここは少しややこしいです。粘性は流体がどれだけネバネバしているかを表す指標です。粘性が小さいとサラサラした流体(水など)で、粘性が大きいとネバネバした流体(マヨネーズなど)になります。粘性とは流体粒子が周りの流体粒子を引きずろうとする力です。粘性が大きいネバネバの流体ほど周りの流体を引きずって流れていそうなのはイメージできると思います。
ここで下図のように、x軸に平行でy方向に速度分布を持つ流れを考えましょう。
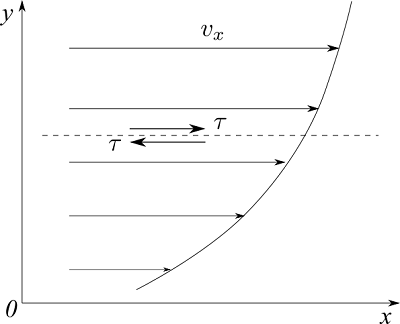
流体中にとったx軸に平行な面には、反対向きに同じ力$\tau$が作用しています。これをせん断応力といい、速度勾配$\partial v_x/\partial y$と粘性係数$\mu$に比例しています。
$$\tau = \mu \frac{\partial v_x}{\partial y} \tag{5-15}$$
これをニュートンの粘性法則と言います。一般的に、y方向の速度成分も持つ場合、せん断応力は次のように表されます。
$$\tau_{xy} = \tau_{yx} = \mu ( \frac{\partial v_y}{\partial x} + \frac{\partial v_x}{\partial y}) \tag{5-16}$$
また、面に垂直な法線応力は同様に、
$$\tau_{xx} = 2 \mu \frac{\partial v_x}{\partial x} \tag{5-17}$$
$$\tau_{yy} = 2 \mu \frac{\partial v_y}{\partial y} \tag{5-18}$$
と書けます(※)。
※圧縮性を考えると法線応力には更に付随した項が現れますが、ここでは無視しています。
ここでまた、微小流体領域を考えます。各面にかかる応力は下図のようになります。
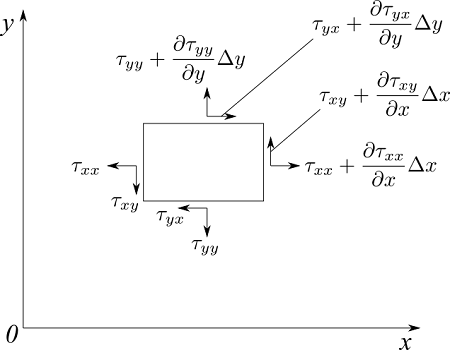
圧力項の導出と同様に考えると、x方向の正味の力は次式で表せます。
(5-19)式に(5-16)、(5-17)式を代入し整理すると、
となります。ここで、非圧縮性流体を考えると、右辺第二項は(5-8)式よりゼロとなるので、
$$F_x = \mu (\frac{\partial^2 v_x}{\partial x^2} + \frac{\partial^2 v_x}{\partial y^2}) \Delta x \Delta y \tag{5-21}$$
と表せます。y方向についても全く同様に計算すると結局、粘性力は
$${\bf F} = \mu \nabla^2 {\bf v} \Delta x \Delta y \tag{5-22}$$
となります。
流体にかかる力は他にも気液二相流であれば表面張力などもありますが、ここでは簡単のために考えないことにします。
これで、すべての力が求まりました。(5-10)、(5-11)、(5-14)、(5-22)式を組み合わせて、両辺を$\rho \Delta x \Delta y$で割ると、(5-2)式のナビエ=ストークス方程式が導けました。
ラグランジュ微分
最後に、右辺に出てくる$D/Dt$という時間微分について説明しておきます。これは、流体とともに移動する流体粒子に乗って見たときの時間変化を表すもので、ラグランジュ(Lagrange)微分と呼ばれています(物質微分とも言います)。一般的に数式で表すと
と書けます。
右辺に出てくる$\partial \phi / \partial t$は空間に固定された座標で見たときの時間変化です。これはオイラー(Euler)微分と呼ばれます。格子法の流体解析では、空間に固定されたメッシュ上で離散式をたてるため、オイラー的に書かれた方程式を使います。このとき第二項目の$({\bf v} \cdot \nabla) \phi $が対流項(移流項)となります。
まとめ
流体の基礎方程式である連続の式とナビエ=ストークス方程式を導出して説明しました。数式満載でややこしかったかも知れませんが、基礎式がどのような意味を持っているかイメージできていると物理現象を考える上でとても役に立ちます。
次回からはSPH法の考え方について具体的に説明していきたいと思います。

