前回はクランク=ニコルソン法を紹介し、計算精度について説明しました。
今回と次回で、2次元の熱伝導の問題を解いてみたいと思います。そして最後には温度が変化する様子をアニメーションにしてみましょう。本日は熱伝導方程式を2次元に拡張し、プログラムでの2次元データの扱いについて説明します。
目次
問題
前回まで1次元の熱伝導の問題を解いてきました。これを2次元に拡張してみます。
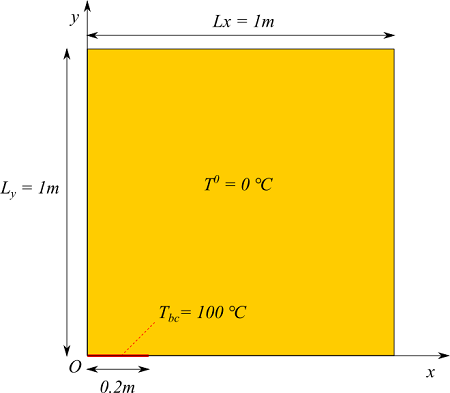
今度は2次元の板の熱伝導の問題です。
2次元熱伝導方程式
まずは数式を考えましょう。きちんと導出からやろうとすると、前と同じように微小体積の熱の出入りを考えてやればよいです。方程式としては、1次元の熱伝導方程式の空間項に $y$ 方向の空間微分が追加された式となります。
これが2次元熱伝導方程式です。
離散化
次に(1)式を数値的に解くために離散化を考えます。今度は空間に $y$ 方向が加わったので、この方向にも離散化してみます。
$y$ 方向を $\Delta y$ の幅で分割して離散化すると図のようになります。
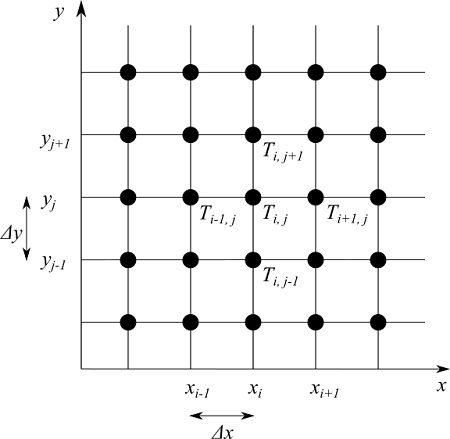
ここで、$x$ 方向の点の添字を $i$、$y$ 方向の点の添字を $j$ として、位置 $(x_i, y_j)$ の温度を $T_{i,j}$ と書くことにします。
時間方向にはこれまでと同じように上付きの添字 $n$ をつけて、$T_{i,j}^n$ とします。
完全陰解法
(1)式を解く数値計算法ですが、ここでは完全陰解法を使うことにしましょう。(1)式を完全陰解法で表記すると、
となります。空間の差分をとるときは、微分する方向の点に対して差分をとっていけばよいです。
(2)式を $T_{i,j}^{n+1} $ について整理すると最終的に次式のようになります。
ここで、$c_x = \alpha \Delta t/ \Delta x^2$、$c_y = \alpha \Delta t/ \Delta y^2$。
あとは(3)式をガウス=ザイデル法で解いていけば解が求まります。
どうでしょうか、2次元への拡張はそれほど難しくはないと思います。これまでの式に機械的に当てはめていけばよいのです。
プログラミング
ここまで出来たらあとはプログラミングしていくだけですが、今回のように2次元のデータはどのように扱えばよいでしょうか。
これまでは一次元のデータを配列 temp[i] を使って表してきました。2次元のデータも配列で表します。この配列は2次元配列と呼ばれます。
2次元配列の要素は temp[i][j] のように表します。$T_{i,j}$ と全く同じように考えればよいです。2次元配列は次のように箱が並んでいるとイメージしてください。
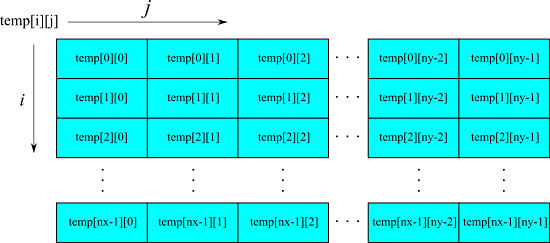
Pythonでは、要素数が nx個×ny個で、全ての値が 0.0 の2次元配列を作るためには、
temp = np.zeros((nx, ny))値が100.0 の2次元配列を作るには、
temp = np.full((nx, ny), 100.0) と書きます。
また、全ての要素に対して処理をしようとすると、
for i in range(nx):
for j in range(ny):
temp_old[i][j] = temp[i][j]のように、i と j でforループを回します。
さあこれだけの情報があれば、以前作った完全陰解法のプログラムを2次元に拡張できると思います。ぜひチャレンジしてみてください。
まとめ
本日は2次元熱伝導方程式へ拡張を行い、2次元データをプログラムでどう扱えばよいかを説明しました。
さて次回はいよいよ最終回です。2次元平面で熱が伝わっていく様子をアニメーションにする部分を加えてプログラムを完成させます。
