前回は熱伝導方程式を導きました。
今回はこの方程式を解くための数値計算法について説明します。
目次
差分法
前回導いた熱伝導方程式は
$$\frac{\partial T}{\partial t} = \alpha \frac{\partial^2 T}{\partial x^2} \tag{1}$$
という微分方程式でした。この式をよく見ると、前シリーズで解いてきた微分方程式によく似た形をしています。左辺の温度 $T$ は時間 $t$ の微分(時間変化)になっているので、右辺が分かればオイラー法やルンゲ=クッタ法で計算できそうな気がします。
しかし、温度 $T$ は空間分布(場所ごとに違う温度)を持っているので、それをどうしたらよいのでしょうか?
離散化
まず、数値計算では空間を分割して考えます。例えば、今回の問題は長い棒なので、図のように棒を $Δx$ の幅で分割してみます。

すると何個かの点に分けられますが、この分割した一点一点で値を計算することにします。ここで、$i$ 番目の点の座標を $x_i$ としておきます。このように、空間を分割して考える方法を離散化といいます。
離散化は空間だけではありません。時間に対しても行います。時間は $\Delta t$ で分割して離散化します。$\Delta t$ は以前でてきた時間刻みに相当します。
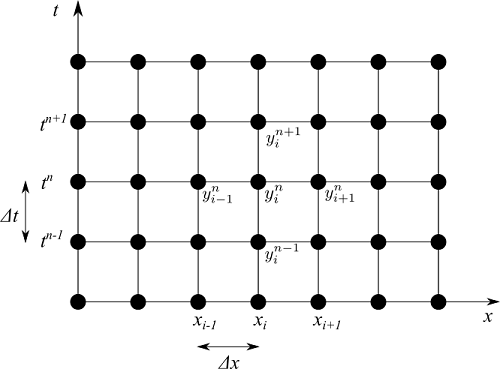
ある時刻を $t^n$ とすると、一つ前の時刻は $t^{n-1}$、一つ後の時刻は $t^{n+1}$ と表します。ここで、時刻 $t^n$ における位置 $x_i$ の値を $y_i^n$ と書くことにします。
このように、離散化をすると空間でも時間でも分割された点で考えることができます。
微分の表し方
解きたい方程式は微分方程式なので微分というのが必ず出てきます。微分はこれまで学んできたように、時間変化や勾配(傾き)といった何かの変化量をあらわしています。
次のような微分を考えましょう。
$$ \frac{\partial y}{\partial x} $$
これは、$y$ を $x$ で微分した量です。($\partial$ は前回説明したように、偏微分を表します。 $d$ の記号の微分は常微分といいます。正確には2つは違うものなのですが、この講座で出てくる範囲ではあまり違いはないので、似たものだと思っておいてください。)
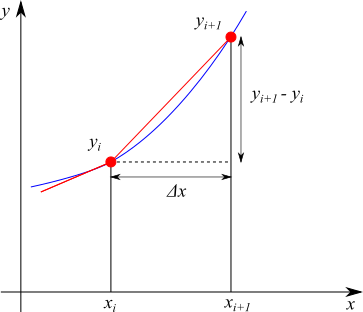
図のように $x_i$ のときの $y$ を $y_i$、$x_{i+1}$ のときの $y$ を $y_{i+1}$ とすると、この傾きは
$$\frac{y_{i+1}-y_i}{\Delta x}$$
と表すことができます。つまり、$x_i$ での微分は
$$ \left. \frac{\partial y}{\partial x} \right|_i = \frac{y_{i+1}-y_i}{\Delta x} \tag{2}$$
と書けます。$i$ のときの微分を $i$ と $i+1$ のときの値を用いて表しています。このような書き方を前進差分と呼んでいます。
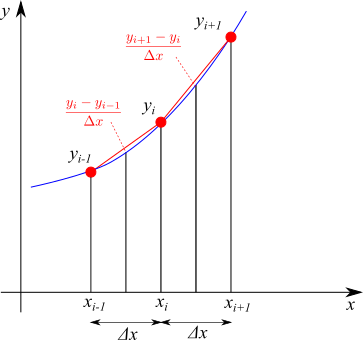
傾きを表す方法は他にも考えられます。$i-1$ のときの値を用いて表すと、
$$ \left. \frac{\partial y}{\partial x} \right|_i = \frac{y_i-y_{i-1}}{\Delta x} \tag{3}$$
これは後退差分と呼ばれています。
さらにもう一つ、$i$ を挟む $i-1$ と $i+1$ の値を使うと、
$$ \left. \frac{\partial y}{\partial x} \right|_i = \frac{y_{i+1}-y_{i-1}}{2\Delta x} \tag{4}$$
となり、中心差分と呼ばれる方法です。
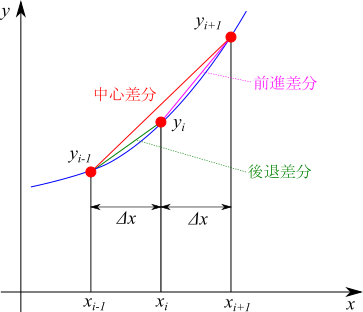
微分を表すとき、どの差分を使えばよいかはケースバイケースです。ここでは、差分にはこれらの種類があるということを覚えておきましょう。
2階微分の表し方
では、(1)式の右辺の2階微分はどう書けるでしょうか?
前回、2階微分は勾配の勾配の形をしていると言いました。つまり、
と表すことができます。$i+1/2$、$i-1/2$ は $i$ を挟む前後の傾きを表しています。
この傾きを差分で書くと、
となります。これは2階中心差分と呼ばれています。
2階微分も前進や後退の形で差分を書くこともできますが、ここでは使わないので詳しくは触れないことにします。
熱伝導方程式を差分で書く
では、(1)式の熱伝導方程式を差分形で書いてみましょう。
時刻 $t^n$ 、位置 $x_i$ の点について考えます。この点の温度は $T_i^n$ です。
(1)式左辺の時間微分は(2)式の前進差分を使います。すなわち 時刻 $t^n$ と次の時刻 $t^{n+1}$ の値を使って表します。また、右辺の空間微分は(6)式の2階中心差分を用います。時刻は $t_n$ の値を使います。すると(1)式は次のように書くことができます。
(7)式を変形すると、次のようになります。
この式を見ると、時刻 $t^{n+1}$ の温度 $T_i^{n+1}$ は、一つ前の時刻 $t^n$ の値を用いて計算できることがわかります。また、空間的には位置 $x_i$ とその両隣の $x_{i-1}$、$x_{i+1}$ の値を使って計算できます。
ここで、(8)式を見て何か気が付かないでしょうか?
この形はこれまでやってきたオイラー法とよく似ています。そうなのです、オイラー法は時間に対して前進差分で表したものなのです(前進オイラー法ともいいます)。
まとめると、この数値解法は時間に対しては前進差分、空間に対しては中心差分を使っているのでFTCS(Forward-Time Centered-Space)法と呼ばれています。
オイラー法あれば今までたくさんやってきたので、プログラミングもイメージがつくと思います。時刻0で初期値として温度の空間分布を与えてやれば、あとは芋づる式に時々刻々値が求まりますね。このように現在の値だけから一つ先のステップが計算できてしまう方法を陽解法と呼んでいます。
(8)式は離散化された空間の各点について成り立ちます。つまり各点の式を連立させて解くと、空間的にも時間的にも解が求まるのです。
まとめ
今回は熱伝導方程式を離散化して差分で表す方法を説明しました。そして出てきた差分式はオイラー法の形になっていることがわかりました。
いよいよ次回からPythonを使ってプログラミングしてみたいと思います。
