目次
はじめに
さあ、今回より「科学技術計算講座」の第3回シリーズが始まります。
これまで、時間変化する量を微分方程式の形で表し、オイラー法やルンゲ=クッタ法といった数値計算法で計算してきました。このシリーズでは、空間分布を持つ量を計算してみたいと思います。
今回シミュレーションする題材は、熱伝導です。身の回りのモノや自然現象を理解するうえでは、熱の移動は欠かせません。熱がどのように空間を伝わっていくのかを知ることはとても重要なことです。
このシリーズでは熱伝導のシミュレーションをとおして、空間分布を持つ量の離散化方法、陽解法や陰解法といった数値計算方法を学んでいきます。
問題
早速、今回解きたい問題を示しておきましょう。
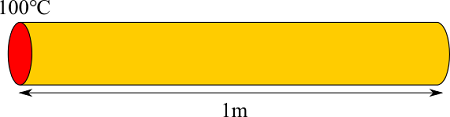
銅の棒の温度変化を求める問題です。シリーズ第1回目で、鉄球の温度変化を求めましたが、あれと似ています。しかし、この問題は長い棒の一方の端だけを熱するというものです。当然最初のころは全体的に温度が低いですが、端から徐々に熱が伝わっていき温度が高くなるとイメージできます。このような問題は空間的な温度分布を考慮しなくてはなりません。
熱が物体の中を伝わっていく現象は、熱伝導と呼ばれています。つまり、空間的な温度分布とそれが時間的にどう変化していくかを同時に解かなくてはなりません。
熱伝導方程式の導出
まずは、今回解く方程式を導出してみましょう。これまでやってきたように、方程式を導くには解きたい対象の時間変化を考えて行くとよいです。
次の図のように棒の中の一部分を考えます。これは、面積 $A$、幅 $\Delta x$ という微小な領域とします。この体積は $A \Delta x$ です。棒なので1次元的に考えます。一方の端の位置を $x$ とすると、もう一方の端は $x + \Delta x$ となります。
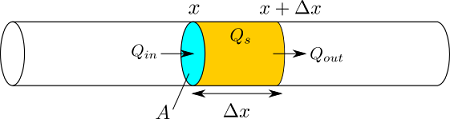
この微小領域の熱の時間変化を考えましょう。熱量の時間あたりの変化を $\Delta Q$、時間あたりに領域に入ってくる熱量を $Q_{in}$、出ていく熱量を $Q_{out}$とします。また、微小領域の内部で時間あたりに発熱する量を $Q_s$ とします。すると、次の式が成り立ちます。
$$ \Delta Q = Q_{in} - Q_{out} + Q_s \tag{1}$$
それぞれの熱量がどのように表されるか考えましょう。まず、左辺の時間変化は
$$\Delta Q = \rho C_p \frac{\partial T}{\partial t} A \Delta x \tag{2}$$
となります。$\rho$ は密度、$C_p$ は比熱、$T$ は温度、$t$ は時間を表します。これは微小領域の熱エネルギーが $\rho C_p T A \Delta x $ であり(*)、以前見てきたように時間変化は微分で表されるからです。( * 質量が $\rho A \Delta x$で、それに比熱 $C_p$ を掛けると熱容量、さらに温度 $T$ を掛けると熱量になる。)
ここで、微分の記号が $d$ ではなく $\partial$ になっていますね。これは、偏微分と呼ばれる微分を意味します。今回の問題では温度 $T$ は時間変化するだけでなく、空間分布を持っています。これまでのシリーズで出てきた量は時間変化するだけでした。変化が一つの量に限られる場合は微分は $d$ で表し、時間変化と空間変化のように複数で変化する場合は $\partial$ の記号で表します。
次に領域に入ってくる熱量はどうでしょうか。熱は温度が高い方から低い方に移動していきます。つまり、熱量は温度勾配があると移動します。温度勾配というのは温度の空間変化、すなわち温度の空間微分 $\partial T/ \partial x$を表します。また温度勾配が大きいと移動する熱量も大きそうです。そこで、移動熱量は温度勾配に比例していると仮定します。さらに、その熱量は面積 $A$ にも比例しています。したがって、領域に入ってくる熱量は
$$Q_{in} = - \lambda \left. \frac{\partial T}{\partial x}\right|_x A\tag{3}$$
と書けます。$\lambda$ は比例定数ですが、一般に熱伝導率と呼ばれています。$|_x$ という記号は、温度勾配が $x$ の位置での値であることを意味しています。なお、マイナスの符号がついていますが、熱は温度の高い方から低い方へ移動するため、勾配に対して負の方向になるからです。ちなみに、(3)式はフーリエの法則(Fourier's law)と呼ばれています。
では、領域から出ていく熱量はどうなるでしょうか。これは(3)式と同じで、出ていく面での温度勾配を使って表されます。
$$Q_{out} = - \lambda \left. \frac{\partial T}{\partial x}\right|_{x+\Delta x} A\tag{4}$$
最後に領域内で発生する熱量ですが、単位時間、単位体積あたりに発生する熱量を $q$ とすると、
$$Q_s = q A \Delta x \tag{5}$$
と書けます。
(2)~(5)式を(1)式に代入して、
整理すると、
となります。
ここで右辺第1項を見てみると、温度勾配の $\Delta x$ での変化、すなわち温度勾配の勾配の形をしています。これは2階微分といい、次の形で書きます。
$$\frac{\partial^2 T}{\partial x^2}$$
これを用いて(7)式を書き直すと、
の形の1次元非定常熱伝導方程式になります。
最後に、(8)式を扱いやすいように変形しておきます。問題から、内部の発熱はないので $q=0$ とし、係数を右辺にまとめると、
$$\frac{\partial T}{\partial t} = \alpha \frac{\partial^2 T}{\partial x^2} \tag{9}$$
となります。$\alpha=\lambda/(\rho C_p)$ は熱拡散率と呼ばれています。これが今回解く微分方程式です。
式の単位について
(9)式の単位について触れておきます。
温度 $T$ [K]、時間 $t$ [s]、長さ $x$ [m]とすると、$\partial T/\partial t$ は[K/s]、$\partial^2 T/\partial x^2$ は[K/m2]、したがって 熱拡散率 $\alpha$ は [m2/s] の単位を持っています。
また、熱伝導率 $\lambda$ は [W/(m K)]、密度 $\rho$ [kg/m3]、比熱 $C_p$ [J/(kg K)] です。
まとめ
本日は熱伝導方程式を導出しました。熱伝導方程式と同じ形をした微分方程式は他にもいろいろあります。少しややこしいですが、このように何かの量の出入りで考えていくと、方程式を導くことができます。
次回はこの方程式を数値計算で解くための解法を考えてみたいと思います。
