前回はルンゲ=クッタ法のプログラムを作り、オイラー法と計算精度を比較しました。
今回からルンゲ=クッタ法を用いて地球の軌道を計算するプログラムを作っていきます。本日は、地球のような惑星がどのような法則で運動しているか考え、計算に必要な方程式を立ててみたいと思います。
目次
万有引力
自分自身を含めて身の回りの物体には重力が働いているのは、皆さんご存知のとおりです。これは、物体が地球に引っ張られているということです。
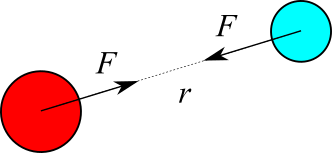
質量 $M$ と 質量 $m$ を持つ物体が距離 $r$ 離れている場合、そこには次のような力 $F$ が働いています。
$$F=-G \frac{Mm}{r^2} \tag{1}$$
ここで、Gは万有引力定数といい
$$G=6.674 \times 10^{-11} \rm{[m^3/(kg \ s^2)]}$$
です。この力は引力を表していて、お互いを引き寄せる方向に働く力です。いわゆるニュートンが発見したという万有引力の法則です。
この式を見ると、力は2つの物体の質量に比例しています。これは質量が大きいほど大きな力が働くことを意味します。また、力は距離の2乗に反比例しています。つまり、距離が離れると急速に力は小さくなります。なお、この力は2つの物体があると、お互いに引きつけ合う方向に働きます。
重力は物体が地球に引っ張られる力として感じていますが、ありとあらゆる物体の間でこの引力は働いています。ただ、その大きさがとても小さいため通常では感じません。60kgの体重の2人の人が1m離れて立っていた場合の万有引力の大きさは、(1)式から $2.4 \times 10^{-7}$ N 程度にしかなりません。100 g の物を支える力がだいたい1Nなので、はるかに小さな力です。逆に地球など大きな質量の物体との間の引力(重力)は、大きな力として感じることができます。
惑星の運動
では、地球のような惑星の運動を考えてみましょう。ここでは、太陽は原点 $O$ に位置しているとします。そして、その周りの2次元平面を惑星が運動していると考えます。太陽の質量を $M$、惑星の質量を $m$ とします。
ここで、惑星の位置を $\vec{r}$ とします。新しいのが出てきましたね。$\vec{r}$ はベクトルです。ベクトルというのは、矢印で表されます。これは方向と大きさを持つ量です。位置をベクトルで表すというのは、惑星の位置を座標で表していると思ってください。
$$\vec{r} = (x, y) \tag{2}$$
が惑星の位置ベクトルです。
次に惑星の速度を $\vec{v}$ とします。これも速度を表すベクトルです。速度も2次元だと x成分、y成分を持っているので、
$$\vec{v}=(v_x, v_y) \tag{3}$$
と表せます。
なぜベクトルで表すかというと、物理の問題はベクトルを使うと、とても都合がよく便利だからです。今は2次元平面で考えているので、x と y の2つの座標で考えますが、3次元空間なら3つの座標が必要です。それぞれ各成分に分けて運動方程式を作っていくと、式の数も多くなり大変です。その点、ベクトルを使うとスッキリ書くことができます。
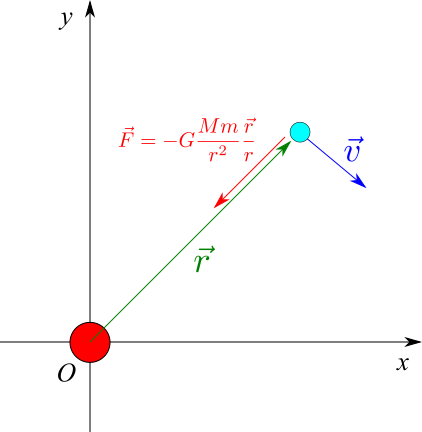
さて、惑星に働く力はどうなるでしょう、(1)式をベクトルで表すと、
$$\vec{F}=-G\frac{Mm}{r^2} \frac{\vec{r}}{r} \tag{4}$$
となります。矢印のない $r$ はベクトルの大きさ、つまり太陽からの距離を表しています。最後の $\vec{r}/r$ のところが方向を表しています。方向は $\vec{r}$ の向きですが、$r$ で割っているので長さが 1 となり、方向だけを表します。全体にマイナスがついているので、この方向とは反対向きに力が働いていることを意味します。なお、この力も成分で表すと、
となります。
この惑星に働く力はこれだけです。実際には、太陽系には多くの惑星や衛星、小惑星などがあるので、他からの引力も働いていますが、今は太陽からの引力のみを考えましょう。
力がわかったので、運動方程式を立てることができますね。この惑星に働く運動方程式は、
$$m \frac{d \vec{v}}{dt}=-G\frac{Mm}{r^2} \frac{\vec{r}}{r} \tag{6}$$
$$\frac{d \vec{r}}{dt}=\vec{v} \tag{7}$$
となります。実際には、それぞれ2成分で表すので4つの式が必要ですが、ベクトルを使うとこのようにスッキリ書くことができます。
方程式の無次元化(規格化)
運動方程式が出来たので、これを数値計算で解いていけばよいのですが、その前に少し方程式を変形したいと思います。ここでやるのは、方程式の無次元化(規格化)という作業です。
(6)式の $G$ は $6.674 \times 10^{-11} \rm{m^3/(kg \ s^2)}$ という、たいへん小さな値です。一方で、太陽の質量は $M = 1.989 \times 10^{30} \rm{kg}$ という、とてつもなく大きな値です。地球と太陽の距離も $r = 1.496 \times 10^{11}\rm{m}$ という大きな数値です。また、地球の公転周期は $3.154 \times 10^7 \rm{s}$ という値になります。このように大きな数値や小さな数値で計算していくと、思わぬ数値誤差を生み出すことがあります。また、値を入力したり、出力された値を評価するのもややこしいです。
このような場合には、ここで行う無次元化という作業を行います。
まず、距離 $r$、速度 $v$、時間 $t$ を次のように表します。
$$r = r_0 \ r_* \tag{8}$$
$$v = v_0 \ v_* \tag{9}$$
$$t = t_0 \ t_* \tag{10}$$
ここで、$r_0$、$v_0$、$t_0$ は規格化定数といい、ベースとなる値です。また、$r_*$、$v_*$、$t_*$ は無次元化された値です。例えば、距離のベースを太陽と地球との距離としましょう。そうすると、太陽と地球の無次元化した距離は $r_* = 1.0$ と表すことができます。こうすることで、扱いやすい数値になります。
方程式を無次元化するために、(8)~(10)式を(6)式に代入します。
$$m \frac{d(v_0 \vec{v_*})}{d(t_0 t_*)}=-G\frac{Mm}{(r_0r_*)^2} \frac{r_0\vec{r_*}}{r_0 r_*} \tag{11}$$
定数をまとめて左辺に持ってきて整理すると、
$$\frac{v_0 r_0^2}{t_0 GM} \frac{d \vec{v_*}}{dt_*}=- \frac{\vec{r_*}}{r_*^3} \tag{12}$$
となります。同じように(7)式にも代入して整理すると、
$$\frac{r_0}{t_0 v_0} \frac{d \vec{r_*}}{dt_*}=\vec{v_*} \tag{13}$$
となります。
ここで、(12)式と(13)式の左辺の頭の定数項を 1 と置きます。すると、
$$\frac{d \vec{v_*}}{dt_*}=- \frac{\vec{r_*}}{r_*^3} \tag{14}$$
$$\frac{d \vec{r_*}}{dt_*}=\vec{v_*} \tag{15}$$
のように、係数のない簡単な式で表すことができます。これが無次元化された惑星の運動方程式です。数値計算にはこの式を使います。ベクトルである点を除けば、これまでやってきた微分方程式によく似ていますね。
また先程、定数項を1と置いたので、規格化定数は
$$t_0 = \sqrt{\frac{r_0^3}{GM}} \tag{16}$$
$$v_0 = \frac{r_0}{t_0} =\sqrt{\frac{GM}{r_0}}\tag{17}$$
と表すことができます。$r_0$ は太陽と地球の距離とするので、規格化定数はそれぞれ、
$$ r_0 = 1.496 \times 10^{11}\rm[m]$$
$$t_0 = 5.022 \times 10^6 \rm[s] = 58.13 \rm[day]$$
$$v_0 = 2.979 \times 10^4 \rm[m/s]$$
となります。ちなみに、$v_0$ は地球の公転速度と同じです。また、$t_0$ を $2\pi$ 倍すると公転周期(365日)となります。つまり、無次元量で考えると、地球は太陽から距離 $r_* = 1.0$ のところを速度 $v_* = 1.0$ で回転していて、$ t_* = 2 \pi$で一周するということになります。
このように、無次元化の操作をすることで、わかりやすい数値で考えることができるようになります。
まとめ
今回は惑星の運動方程式を考え、無次元化して数値計算で使う式を導きました。また、ベクトルを使ってずいぶんシンプルな式になりました。数式がたくさん出てきたので頭が痛くなった人もいると思いますが、意外と簡単な式なのでこれまでの知識を使えばプログラミングできそうです。
さて、次回はいよいよPythonでプログラムを作ってみたいと思います。
