前回までで、Pythonを使って一分子反応をオイラー法でシミュレーションするプログラムが一通り完成しました。
今回は、計算した結果の精度についてお話したいと思います。
目次
計算結果は正しいか?
簡単なプログラムで一分子反応の計算をすることができましたが、この計算結果は本当に正しいのでしょうか?
シミュレーションなどの数値計算結果をグラフやきれいなアニメーションなどで見せられたりすると、何も考えずにこの結果は正しい、実際こうなるんだと思ってしまいがちです。今回計算した一分子反応の計算結果はどうでしょうか。物質Aの微分方程式は次のように書けました。
$$\frac{d [\rm{A}]}{dt} = -k [\rm{A}] \tag{1}$$
実はこの方程式は、手で積分して計算することができます。この解は、
$${[\rm{A}]} = e^{-k t} \tag{2}$$
となります。つまり、ある時刻 $t$ のAの濃度は(2)式で計算できてしまいます。このような解を厳密解とか解析解といいます。では、この厳密解と計算結果を比べてみましょう。
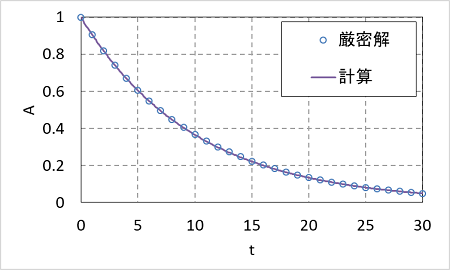
この図は、A濃度の厳密解と計算結果を比べたグラフです。結構ピッタリ一致しています。ということは、この計算結果は悪くなさそうです。
時間刻みの影響
ところで、以前プログラムを作ったときに、時間刻みを dt = 0.1 に設定しました。あのとき、時間刻みを大きくすると、粗い計算になると言いましたが、実際はどうでしょうか。試しに、dt = 5.0 として計算してみましょう。計算結果を同じグラフに書くと、
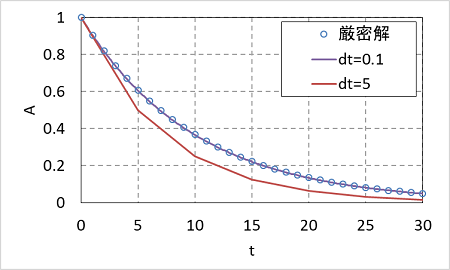
となります。dt = 5 は厳密解から大きくずれてしまうことがわかります。なぜこのようになるかは、オイラー法の考え方をもう一度思い出せばイメージできます。
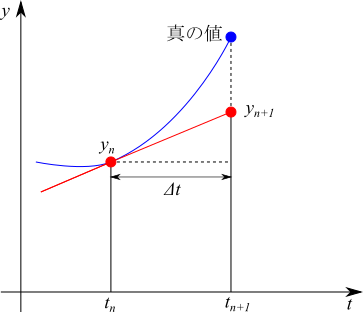
時刻 $t_n$ から、時間刻み $\Delta t$ 進んだ所の値 $y_{n+1}$ は、$t_n$ のときの傾きから求めているわけです。このとき、実際の値は青線をとるとしましょう。青線が $\Delta t$ 進む間に大きくカーブしていれば、オイラー法で求めた $y_{n+1}$ の値は、真の値から大きく外れてしまいます。
このように、時間刻みを大きくとると、計算結果に大きな誤差が生じてしまうのです。では、今回のように 0.1 の時間刻みを取れば、よいのでしょうか?
次の微分方程式を考えてみます。
$$\frac{dy}{dt} = y$$
これをオイラー法で dt = 0.1 で計算してみます。(前回作ったプログラムで k = -1.0 で計算して、Aの結果を見ればこの式と同じです。)この方程式の厳密解は、$ y = e^t$ なので比べてみます。
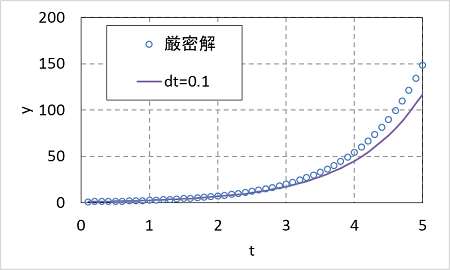
5秒後には厳密解から結構ずれていることがわかります。このように、dt = 0.1 だから正確だというわけではありません。真の値の傾きが大きく変化するようなものは、かなり時間刻みを小さくしないと誤差が大きくなります。また、時間刻みを小さくとりステップあたりの誤差を小さくしたとしても、長くステップ計算をしていくうちに、小さな誤差が蓄積されて、時間が経つと誤差が大きくなる場合もあります。
オイラー法の計算精度
このようにオイラー法は、単純にそのときの傾きから、その一つ先を予測しているので、数値計算法としての計算精度はあまりよくありません。今回はたまたま厳密解と一致した結果が得られましたが、解くべき方程式によっては結果が実際の値からずれてくる場合があります。
ただし、オイラー法は簡単にプログラミングでき計算も早いので、さっと計算して確かめたい場合には良い方法だと思います。そのときに、ここで説明したような誤差を含んでいるということを忘れないようにしてください。
また、今回のように厳密解がわかっていれば、計算結果と比較してみればよいのですが、普通は厳密解はわかりません。(というか、厳密解がわかるものは、数値計算する必要がないので。。。)そこで、一つの方法として、時間刻みをいくつか変えて計算し、結果がある程度変わらなくなることを確かめるというのがあります。時間刻みを小さくしていったときに、結果が変わらないようならひとまずその結果を計算結果とみなすというものです。
実際には、オイラー法よりも計算精度が高い数値解法がいろいろ考えられています。精度がより高い数値解法については、またいずれ説明したいと思います。
もう一度、計算結果は正しいか?
最初の質問に戻ります。「計算結果は正しいか?」という質問の「正しい」とはどういうことでしょうか。この正しいには少なくとも2種類あります。
- 方程式の解が正しく求まっていれば正しい
- 実際の現象と計算結果が合っていれば正しい
1については、これまで説明した数値計算精度の話です。方程式の真の解と誤差が小さければ正しいといえます。
しかし、普通の人は「実際の物質Aの濃度変化と計算結果が合っていれば、シミュレーションは正しい」と言うようです。実をいうと、1で誤差なく答えが求まったとしても、実際の現象と合っている保証はありません。そもそも、解いた方程式が実現象を表現していなかったら、結果が合うはずはありません。また、方程式がうまく出来ていても、初期値や係数の値がずれていたら結果も違ってくるでしょう。さらに言えば、そもそも実現象というのが実験による測定や観測結果のことだとすると、その測定自体の精度が悪ければ、計算との比較すら意味をなさなくなることもあります。
このように、「計算結果が正しい」というのは、何について正しいのかをよくよく考える必要があるのです。その上で、数値計算で出てきた結果を評価しなければなりません。ここの評価がきっちりできていると、数値計算はとても有益なツールとなるでしょう。
まとめ
今回は、オイラー法の計算精度から数値計算の正しさについても説明しました。オイラー法に限らずどんな数値計算法でも何らかの誤差を含んでいます。また方程式や測定自体が含む誤差もあります。誤差の種類もいろいろあるのですが、ここではあまり詳しくはやりません。ひとまず、数値計算には今回説明したような誤差があるのだ、というイメージを持っておいてください。
次回は、一分子反応のプログラムを応用して、同じ微分方程式の形をもつ他の問題を解いてみたいと思います。
