
前回、AnacondaでPythonをインストールしました。
今回から具体的な数値計算の方法に入っていきます。本日は、計算の例題を示して、それがどのような数式で表現されるのかを説明します。
目次
一分子反応
最初の例題として、簡単ですが応用の効く基本となるものにしたいと思います。そこで、次のような問題を考えます。
これは化学の問題です。普通は酸素と水素が結合して水ができるという二分子反応がよくありますが、これは一分子反応といって、ある物質が時間がたつと他の物質に変わるというものです。
化学反応式で書くと、
$$ \rm{A} \rightarrow \rm{B} $$
というとても簡単なものになります。
数式にする
では、この問題を数式で表現するにはどうしたらよいでしょうか?
Aという物質の濃度の時間変化を求めたいので、「Aという物質は時間あたりどれくらいの量がBという物質に変化していくか」という割合がわかれば計算することができそうです。
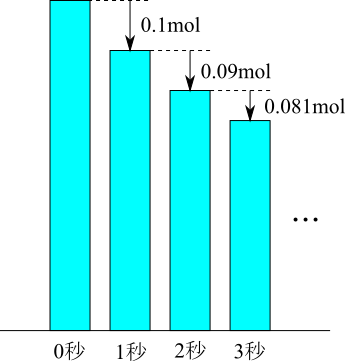
例えば、「Aは1秒あたり10%の割合でBに変化する」ということがわかっていたとしましょう。もし最初、1Lの溶液の中に、Aが1molあったとすると(molは物質量の単位で分子が$6.02 \times 10^{23}$個ある状態が1molです)、1秒で10%減るので1秒後には
$$1 - 0.1 \times 1 = 0.9 \ \rm{mol}$$
になります。だとすると、単純に計算して10秒後にはAは全部Bに変化してしまうでしょうか?
もしそうなら、わざわざコンピューターで数値計算しなくても、手計算で計算できてしまいます。しかし、そう簡単ではありません。なぜかというと、「Aは10%の割合で変化していく」となっているからです。つまり、1秒後に0.9 molになったとすると、次の1秒間では0.9 molの10%すなわち0.09 molがBに変化することになります。したがって、最初から2秒後には、
$$(1 - 0.1 \times 1) - 0.1 \times (1 - 0.1 \times 1) = 0.81 \ \rm{mol}$$
になるという計算です。つまり変化する割合は10%と一定なのですが、変化する量は時間とともに小さくなります。だとすると、Aが全部Bに変わるには10秒よりもっとかかりそうです。
これを計算するには、いきなり数列の問題のように計算していってもよいのですが、それではスマートではありません。数値計算のためには、まずこの現象を数式で表してみます。時間あたりに変化する割合を $k$ とすると、Aが変化する量は、
$$-k [\rm{A}] \tag{1}$$
と表せます。$[\rm{A}]$ は物質Aの濃度です。ここでの濃度はモル濃度といい、1L中に何molあるかというのを表しています。
マイナスなのは、Aは減るからです。変化する割合が $k$ = 0.1 で濃度が $[\rm{A}]$=1 なら、変化する量は単純に掛け算で0.1✕1なので、ここまではいいですね。
これはAが時間あたりに変化する量(変化量)なのですが、時間あたりの変化量というのは次のように表します。
$$ \frac{d [\rm{A}]}{dt} \tag{2}$$
これは高校で習う微分というやつです(忘れた方はなんとか思い出してください)。濃度 $[\rm{A}]$ が時間 $t$ あたりどれだけ変化するかを表しています。(1)と(2)は同じものなので、イコールです。つまり、
$$\frac{d [\rm{A}]}{dt} = -k [\rm{A}] \tag{3}$$
という式ができあがります。これが物質Aがどれだけ変化していくかを表す式です。微分が入っているので、微分方程式といいます。
あともう少し。今度は物質Bについて考えましょう。BはAが減った分だけ増えると考えられます。Aが減った分は(1)式です。Bの変化はAと同じように、
$$ \frac{d [\rm{B}]}{dt} \tag{4}$$
で表すと、Bの式は、
$$\frac{d [\rm{B}]}{dt} = k [\rm{A}] \tag{5}$$
となります。Bは増えるので右辺はプラスです。
まとめると、
$$\left\{ \begin{aligned} \frac{d [\rm{A}]}{dt} &= -k [\rm{A}]\\ \frac{d [\rm{B}]}{dt} &= k [\rm{A}] \end{aligned} \right. \tag{6}$$
となります。これが、問題の一分子反応を表す方程式です。化学では反応速度式といいます。また、$k$ のことを反応速度定数といいます。
これで、今回解きたい問題の数式を表すことができました。
単位について
最後に、この式の単位について説明しておきます。左辺の微分は、濃度を時間で割った形をしているので、
[濃度] / [時間]という単位になります。今、濃度を[mol/L]、時間を[s](sは秒のこと)の単位とすると、
[mol / L / s]がこの式の単位となります。つまり、1 s あたり何 mol/L変化するかというのを表します。右辺は、$[\rm{A}]$が濃度で[mol/L]の単位なので、$k$ は [1/s] の単位を持っていることになります。これは、1 s あたりの変化の割合を表しているのです。
まとめ
一分子反応を例題に、この問題がどのような数式で表されるかを考えました。数式に拒否反応を示す人は、これだけで嫌気がさしたかと思います。でも実は科学技術計算において、この数式に落とし込む作業は最も重要なところなのです。今回と次回の数値計算手法のところまでで、8割仕事が終わったと思って良いでしょう。それくらい重要なところなので、あやふやな所は高校数学を思い出しながらもう一度じっくり考えてみてください。
本日はこれで終了です。次回は、この微分方程式をコンピュータでどのように計算していくかというお話です。
